Chapter 1: Introduction to the Putnam Problem

In this article, we delve into problem 3 from the Putnam exam of 1997, which presents a unique integral that, despite its unconventional appearance, yields a surprisingly neat result. Before proceeding to the solution, it’s advisable to attempt solving the problem yourself.

We might observe that the integral resembles a Taylor series. Let's explore this connection further. The initial series can be expressed as follows:

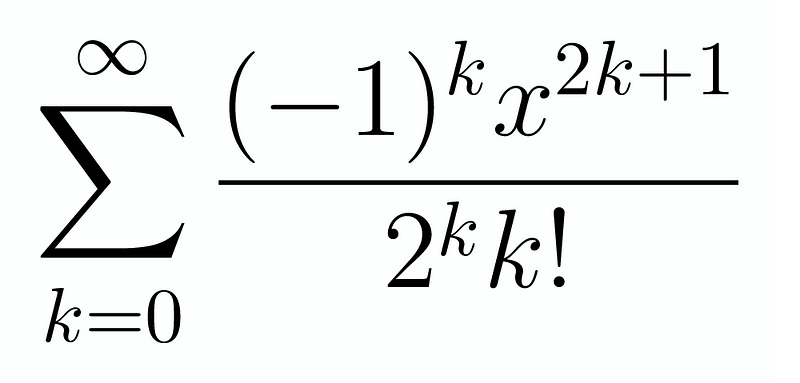
To enhance our understanding, we can recall the Taylor series for the exponential function, which is defined as:

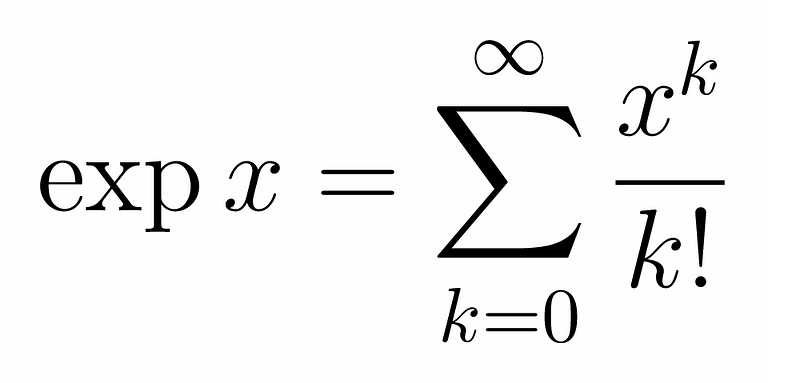
By rearranging the terms in our sum slightly, we can recognize that it transforms into an exponential function. Here’s how it appears:

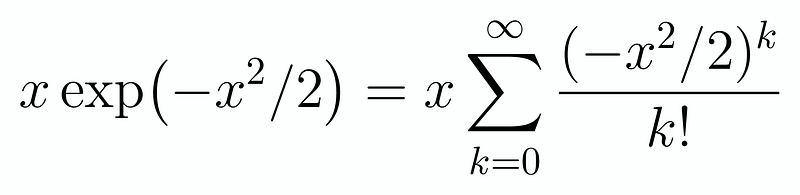
At this juncture, a pertinent question arises: Should we attempt a similar approach for the second series, or is it more effective to convert this into an integral of a sum? While it is feasible to apply the same method to the second series, it does not yield a particularly elegant integral. Therefore, we’ll opt for the latter approach and analyze a more general integral:

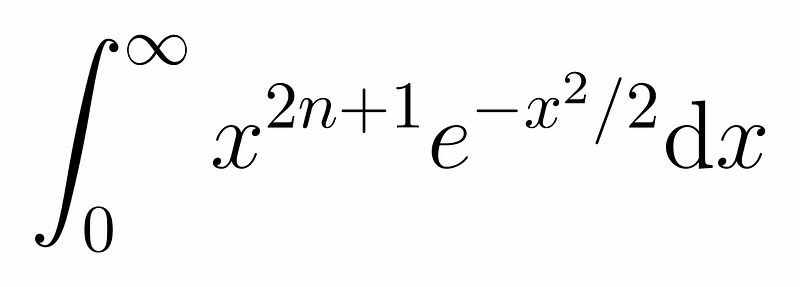
The focus on odd exponents is strategic, as our second series contains only even exponents. Consequently, upon multiplying by ( x ) derived from our first series, we are left with odd exponents. After applying integration by parts once, we arrive at the following equality:

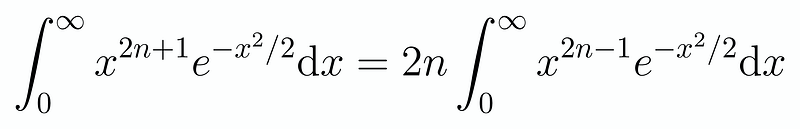
Revisiting our integral, we can simplify it to:

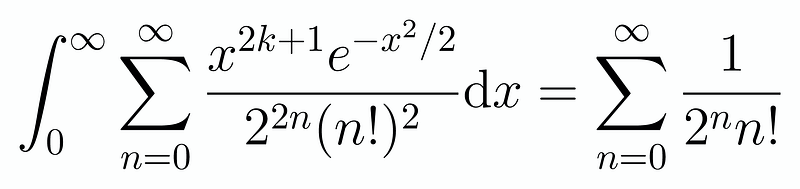
This series is straightforward to evaluate when referencing our Taylor series for the exponential. Specifically, substituting ( x = 1 ) into ( exp(1/2) ) provides us with:

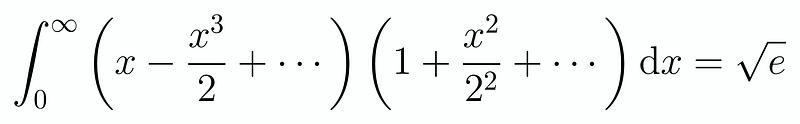
A truly elegant outcome!

Interested in this exploration? Consider supporting us here!