Mastering a Challenging Algebra Puzzle Without a Calculator
Written on
Chapter 1: Introduction to the Algebra Challenge
Welcome to the thirteenth installment in our series dedicated to tricky algebra challenges. In this collection, we explore the delightful world of algebra, featuring problems that cater to all skill levels, from novice to expert.
Before diving into today's puzzle, let’s address the main point. This challenge is not your standard algebra problem; it can be solved quickly with a calculator. However, the twist is that you must rely solely on algebra to find the solution. Essentially, while it may seem like an algebra problem, it is crafted to challenge your algebraic thinking.
So, how will you tackle this algebra conundrum?
Spoiler Alert
If you prefer to solve the problem independently, I suggest you stop reading now, as I will reveal the solution after this section. Once you've given it a try, feel free to continue and compare your method with mine.
Section 1.1: Setting Up the Algebra Challenge
This algebra problem becomes remarkably straightforward when analyzed through an algebraic lens. By taking a closer look, we can express all the relevant numbers in terms of 100:
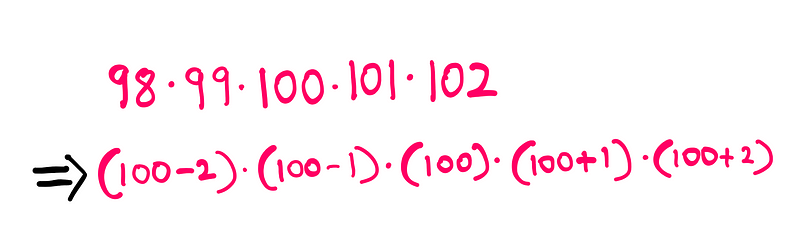
Recognizing Patterns in Algebra
After slightly rearranging the terms, we reach the following expression:
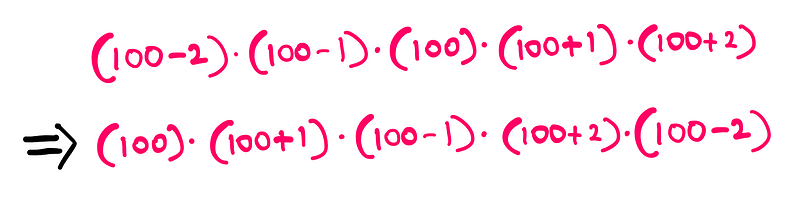
Do you see any recognizable algebraic patterns? If not, don't worry; clarity is just around the corner. To simplify our calculations and embrace the spirit of algebra, let’s substitute 100 with the variable ‘x’:
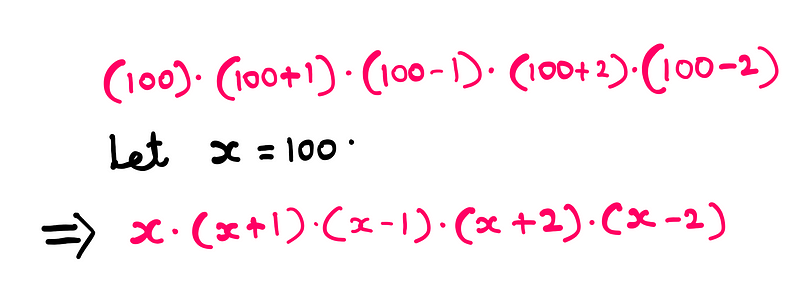
By doing this, we can identify the following algebraic identity:
(a + b) * (a - b) = a² - b²
Applying this identity leads us to the following result:
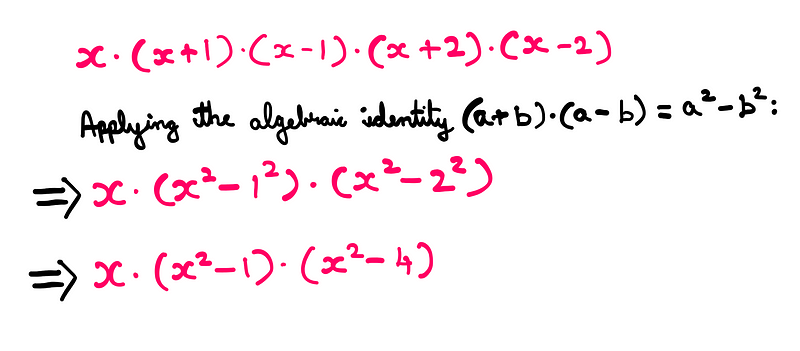
With this step, we are on the brink of solving our problem.
The Solution to the Algebra Puzzle
Now, let's substitute 100 back in for ‘x’ in the expression we derived earlier:
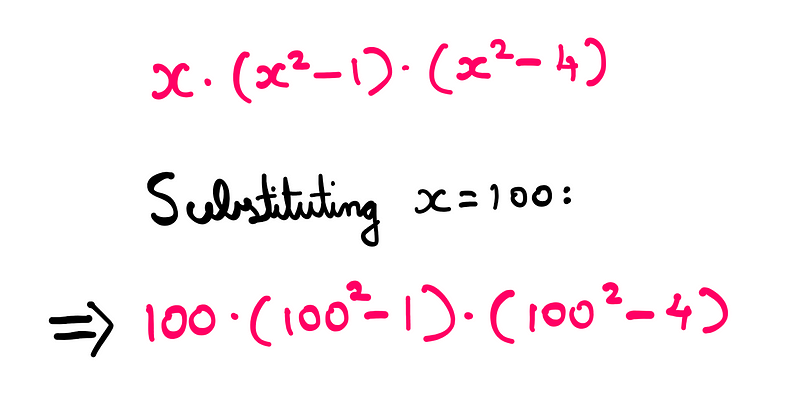
Next, we can proceed with simple cross-multiplication:
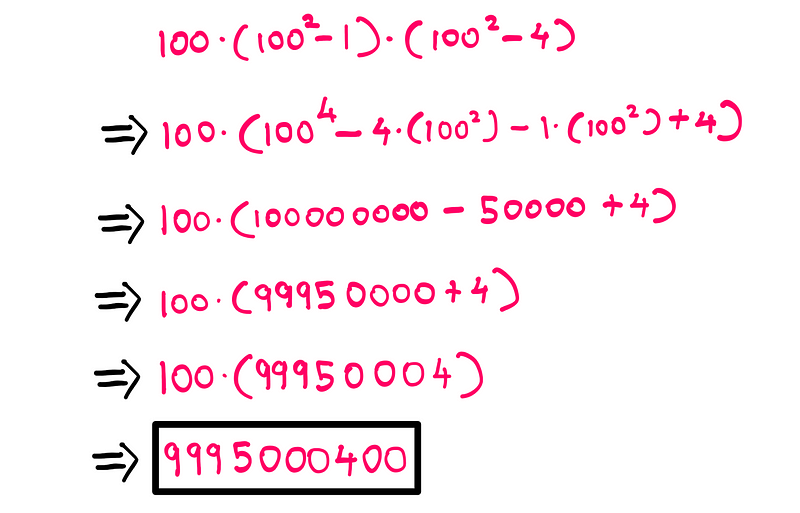
And there you have it! We’ve successfully solved the problem using algebra!
Final Thoughts
The observant reader may note that introducing the variable ‘x’ was not strictly necessary to solve this problem. However, I chose to do so to highlight the underlying pattern for those who might have missed it initially.
Additionally, this problem serves as a practical illustration of how algebra can be applied to relatable real-world scenarios. People frequently encounter multiplication involving large numbers without a calculator, making this approach quite relevant.
I hope you found this engaging and straightforward algebra puzzle enjoyable. If such challenges intrigue you, stay tuned for more in this series. Thank you for reading!
Chapter 2: Engaging with Algebra on YouTube
To further enhance your understanding, check out these videos:
The first video, "A Tricky Algebra Problem with Exponents," provides additional insights into solving algebraic problems creatively.
The second video, "Can you solve this tricky math problem?" challenges you to apply your skills in a fun and engaging way.
If you would like to support future content, consider contributing on Patreon.