Chapter 1: Understanding Spherical Geometry

Spherical geometry presents a fascinating aspect of mathematics, characterized by unique properties, such as the sum of angles in a triangle exceeding 180 degrees. Among its intriguing concepts is the Gauss-Bonnet Theorem, specifically concerning triangles on the surface of a sphere. This theorem can be appreciated through visual representation.

To grasp the concept of a triangle in spherical geometry, consider the visualizations below, which depict the same triangle from different perspectives.

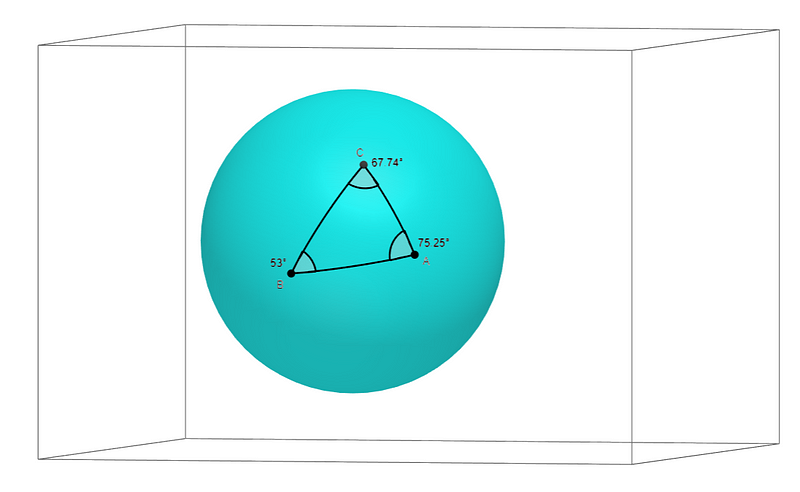
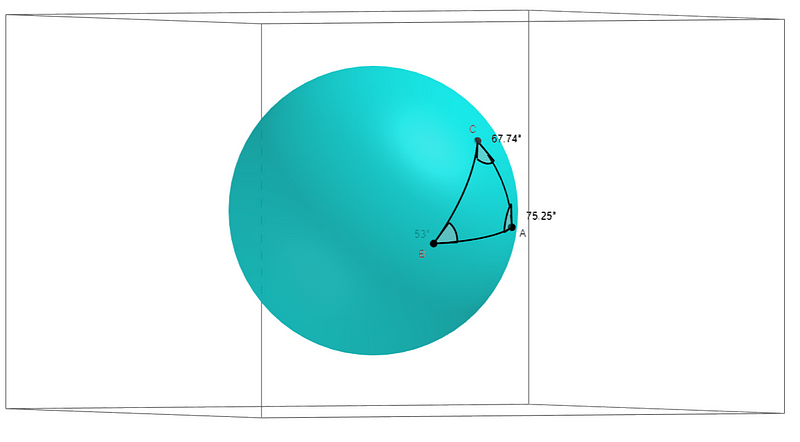
The process of creating a triangle on a sphere involves selecting three points and connecting them. However, defining a "line" on a spherical surface isn't straightforward. Instead, we draw the shortest possible curve between two points. This curve is what we consider when visualizing the triangle's sides.

Next, we analyze the angles formed at each vertex. Since this triangle exists on a sphere rather than a flat plane, determining these angles requires a different approach. As the curves connecting the triangle’s vertices become increasingly parallel, they begin to resemble straight lines, as illustrated below.

This visual representation assists in conceptualizing how angles can be defined within spherical geometry.

Section 1.1: Defining Angles on a Sphere

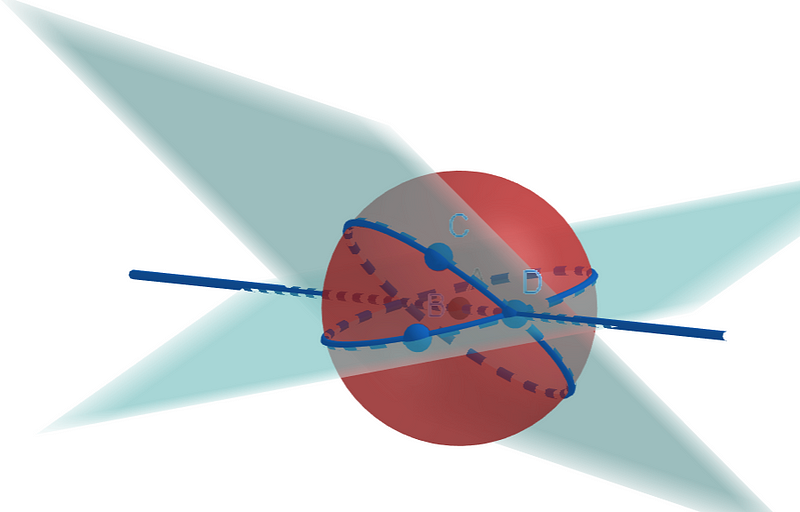
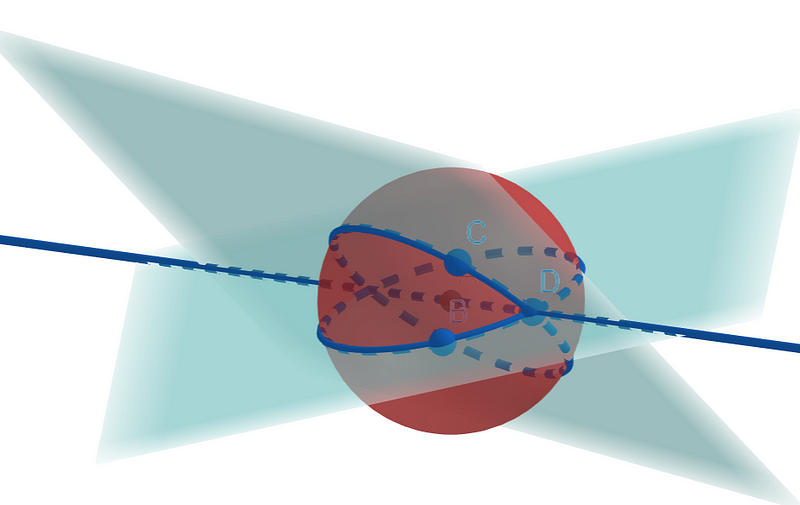
For those keen on a more rigorous definition of angles in spherical triangles, we can delve deeper. By selecting three points—B, C, and D—we can construct a triangle and create three planes using the sphere's center and pairs of these points.

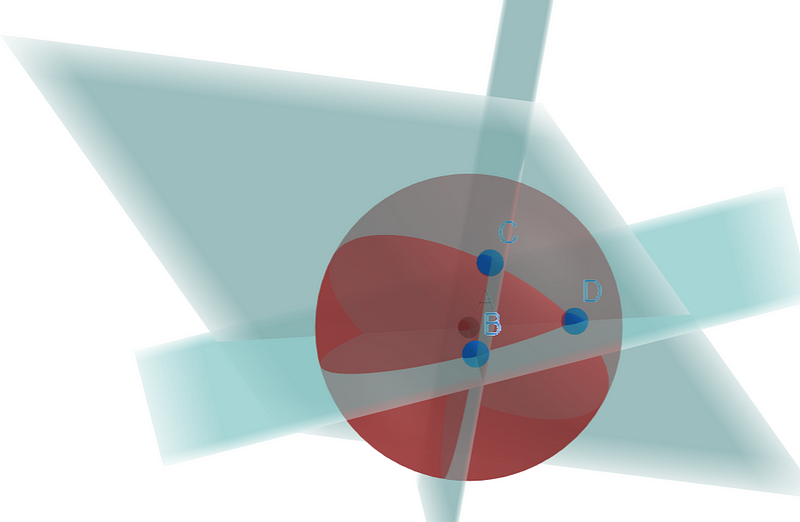
The complexity of this diagram may seem daunting. A simpler illustration can clarify how to form a plane using two points and the sphere's center.

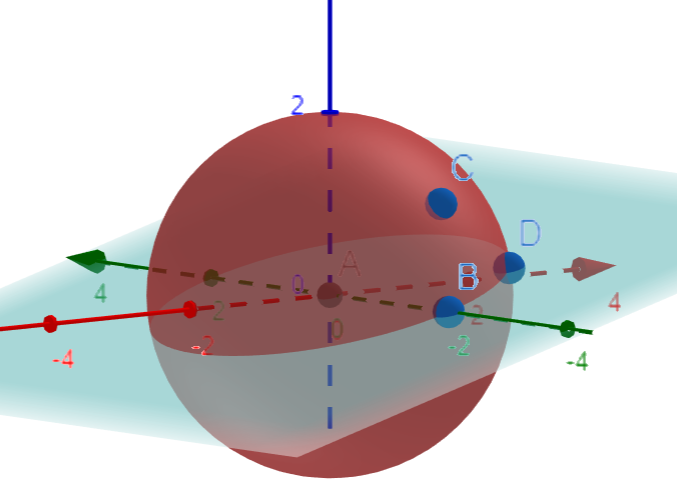
We can subsequently define the angle between two sides of the triangle by referencing these planes, as they function like flat surfaces in three-dimensional space.

Section 1.2: Presenting the Theorem

Now, we arrive at the statement of the theorem. It's important to note that angles are measured in radians, where 2π radians equal 360 degrees, π radians equal 180 degrees, and π/2 radians equal 90 degrees. This is akin to measuring distance in kilometers or miles. However, for those more comfortable with degrees, I will also present the formulas in that format.

If we denote the triangle's angles as a, b, and c, we arrive at the area formula for the triangle:

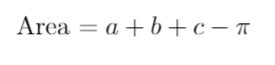
Alternatively, using degrees:

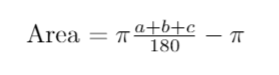
A surprising implication arises from this formula. If the sum of the angles in a triangle equals 180 degrees, then the area would be zero, which is illogical. Thus, we can conclude that the angles of a spherical triangle must total more than 180 degrees, or π radians.

Chapter 2: Proof of the Theorem

To prove the theorem, we will first consider the area of a simpler geometric shape known as a "spherical lune."

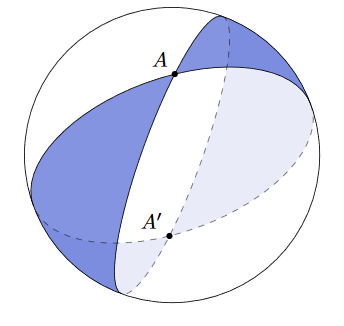
By examining two planes and the area they encompass on the sphere, we find that the total surface area of a sphere is 4π. If the angle between these planes measures c radians, the area between them is 4c. For instance, if the angle is 90 degrees (or π/2 radians), the area captured is 2π, which is half the sphere's total area.

For clarity, when using degrees, the formula becomes less elegant, adjusted by a factor of π.

Now, let’s shift our focus back to the triangle. We can apply a clever technique: by repeating the previous process three times, we can visualize the shaded area representing our triangle, which overlaps in three spherical lunes.

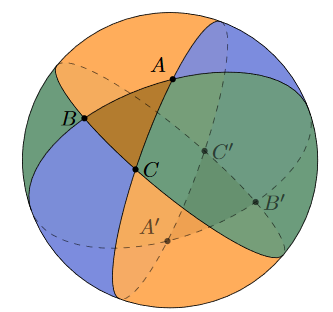
This overlap means the triangle's area is counted three times. By summing the areas of the lunes, we can relate the triangle's area to the total surface area of the sphere. We know the area of each lune is determined by the angle of the triangle's vertices.

Thus, we can derive the final conclusion:

And that concludes our exploration of the Gauss-Bonnet Theorem! If you have any insights or suggestions, feel free to leave your thoughts in the comments below! You can also connect with me on Twitter @ethan_the_mathmo.

The first video, "What is the Gauss-Bonnet theorem?", provides an engaging visual explanation of this fascinating theorem.

In the second video, "Differential Geometry: Lecture 27 part 1: Gauss Bonnet Theorem," we delve deeper into the mathematical intricacies surrounding the Gauss-Bonnet Theorem.