Unveiling the Wonders of Complex Functions and Their Applications
Written on
Chapter 1: Introduction to Complex Functions
This article is the first in a series designed to present the fascinating results of complex analysis in a comprehensible manner. Even if you haven't taken a course in complex function theory, you can still gain valuable insights into this remarkable field. For those studying mathematics or brushing up on their skills, this is an excellent resource, as I'll introduce various intriguing perspectives on the subject.
Before delving into this rich and beautiful topic, let’s establish some foundational concepts.
This paragraph will result in an indented block of text, typically used for quoting other text.
Section 1.1: Fundamental Concepts
In the realm of real-valued functions with a single real variable, continuity and differentiability are contingent upon specific conditions derived from limits approached from only two directions: left to right and right to left. As the real line is one-dimensional, these are the only possible approaches.
For example, to verify continuity, one method is to confirm that the limit of the function as the input approaches a certain value, say a, from the left equals the limit when approaching from the right.
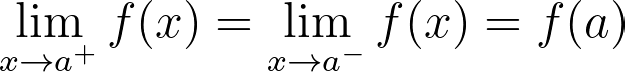
Similarly, differentiability has a two-way condition, but this condition is stronger than that of continuity. The limitation of only two directions renders these properties somewhat weak, as real analysis allows for many pathological functions that may satisfy the differentiability criterion at a point on the real line while lacking a derivative at that point. In fact, the existence of the limit towards that point is not guaranteed!
Moreover, these weak conditions complicate our understanding of such functions, resulting in a lack of powerful analytical tools. However, the scenario shifts dramatically in the realm of complex numbers and their functions, as you will soon discover. The conditions are much stronger, providing us with numerous useful tools and elegant theorems.
Numerous challenges in real analysis can only be addressed using techniques from complex analysis. Before we explore some interesting aspects, let’s clarify a few points. In real analysis, we typically map a possibly infinite interval (or union of intervals) of the real line onto itself. Specifically, the domains of these functions are one-dimensional.
Before focusing on complex functions, I will briefly revisit some properties of complex numbers, along with their geometry and topology.
Section 1.2: Understanding Complex Numbers
The foundation lies in the imaginary unit, denoted as i, which satisfies the equation i² = -1. No real number possesses this property!
Complex numbers can be viewed as a two-dimensional real vector space spanned by the basis of 1 and i. In essence, a complex number takes the form a + bi and adheres to the typical vector space laws, such as the distributive and commutative laws.
Thus, a geometry arises from complex numbers, which have both magnitude and direction (as they are vectors) and can be visualized within a plane known as the complex plane, which is isomorphic to ℝ². For instance, the complex number 3 + 4i corresponds to the point (or vector) (3, 4) in this plane. In a more general sense, a complex number a + bi represents the point (a, b) in the complex plane.
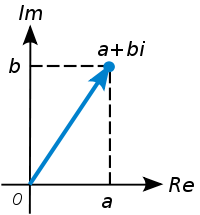
While this vector interpretation of complex numbers is reminiscent of ℝ², there is additional structure due to the ability to multiply complex numbers. Mathematically, this makes them a ring, as vector spaces are abelian groups under addition.
In fact, complex numbers form more than just a ring; they constitute a field since every non-zero element has an inverse, allowing for division. When multiplying two complex numbers, one applies the distributive law, keeping in mind that i² = -1.
Now that we have a grasp on the complex plane, we turn our attention to the study of functions defined over subsets of this plane. Envision a possibly distorted disk with zero or more holes, which may sometimes represent the entire complex plane. Notably, the domains of these functions are two-dimensional, leading to intriguing consequences.
Chapter 2: Holomorphic Functions and Their Properties
The cornerstone of complex analysis is the notion of complex differentiable functions, commonly referred to as holomorphic functions.
As mentioned previously, differentiability implies the existence of a certain limit, but when a function is defined over a two-dimensional domain, there are infinitely many directions from which one can approach a number. This imposes significant restrictions on the set of holomorphic functions, endowing them with remarkable properties.
To illustrate this omnidirectional limit, we can represent a complex function of one complex variable mapping a complex number to another.
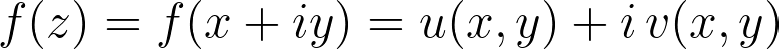
For example, consider the limits along the real and imaginary axes, which yield the same result, demonstrating that the direction of the limit does not matter.
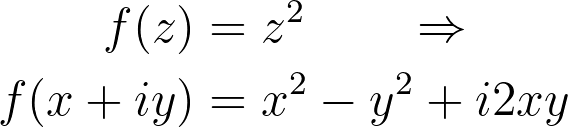
Continuing with this, we can express these limits mathematically, revealing that the two limits must equate.
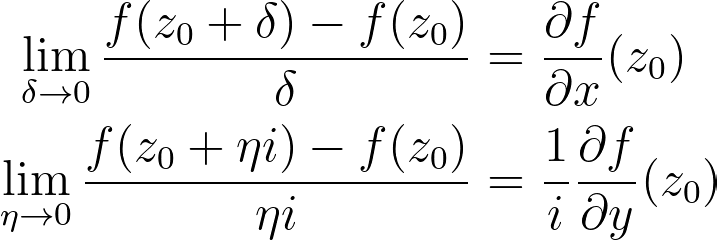
By expanding f into its real components u and v, where f = u + iv, and substituting this into the derived differential equation, we arrive at a system of partial differential equations known as the Cauchy-Riemann equations. This derivation illustrates that every holomorphic function must satisfy these equations, imposing strict requirements on them. The converse holds true with certain continuity considerations.
Additionally, at points where a given holomorphic function’s derivative is non-zero, the function preserves angles, a property referred to as a conformal map, which is a significant and appealing aspect of these functions.
Section 2.1: Properties of Holomorphic Functions
One of the first indications of the intriguing properties of holomorphic functions is the fact that if a function is holomorphic (i.e., complex differentiable) within a domain containing a point p, it is infinitely complex differentiable at p.
This can be succinctly stated: the derivative of a complex differentiable function is also complex differentiable. This assertion is not generally true for real functions.
Section 2.2: Analytic Functions
Consequently, holomorphic functions are also classified as analytic, possessing a convergent power series around any point within their domain, along with a defined radius of convergence. Interestingly, the converse is equally valid; any analytic function is holomorphic. Thus, the terms "holomorphic" and "analytic" are often used interchangeably, although they convey different meanings. We retain both definitions due to the existence of real analytic functions, which do not equate to real differentiability.
As previously stated, a holomorphic function features a power series expansion. Power series possess a radius of convergence, which can be visualized as a disk in the complex plane where this series converges, while at least one point on the disk's boundary causes divergence.
In the subsequent sections, we will explore ways to navigate around troublesome points, thanks to the two-dimensional nature of the complex plane!
Section 2.3: Invisible Symmetries
Before diving into the implications of holomorphy, let’s examine an intriguing aspect: the geometry involved in taking roots—not just polynomial roots, but also square roots, cube roots, and beyond.
Recall that the square root of 4 is defined as 2. However, this question can be reformulated: "What number squared equals 4?" This question is somewhat ill-posed, as there are indeed two numbers that satisfy this equation.
Convention dictates that we refer to the positive square root, but both 2 and -2 are valid square roots of 4.
When considering cube roots, we learn that there is one real cube root for each real number. Yet, this assertion requires modification: while there is precisely one real cube root, two additional roots exist in a different dimension! Specifically, any number (except 0) has three distinct cube roots.
Moreover, any complex (including real) number possesses n distinct n-th roots!
It is vital to note that the additive identity 0 is exceptional in the multiplicative world. If we take multiplicity into account, the aforementioned statement holds true for 0; otherwise, we must exclude it.
What’s even more astounding is that these n roots of a complex number z are symmetrically positioned along the circumference of a circle, with a radius equal to the positive n-th root of the modulus of z, centered at 0.
This symmetry explains why a real number has one real cube root and two real square roots; if these roots must be symmetrically arranged around a circle, one root determines the placement of the others. For instance, one square root of 1 is 1, meaning the other must be -1 due to symmetry.
In a similar vein, one cube root of 1 is 1, while the other two roots are located at the vertices of an equilateral triangle inscribed within the unit circle.
In general, the n roots of 1 form the vertices of a regular n-gon, all lying on the unit circle. These roots are termed roots of unity.
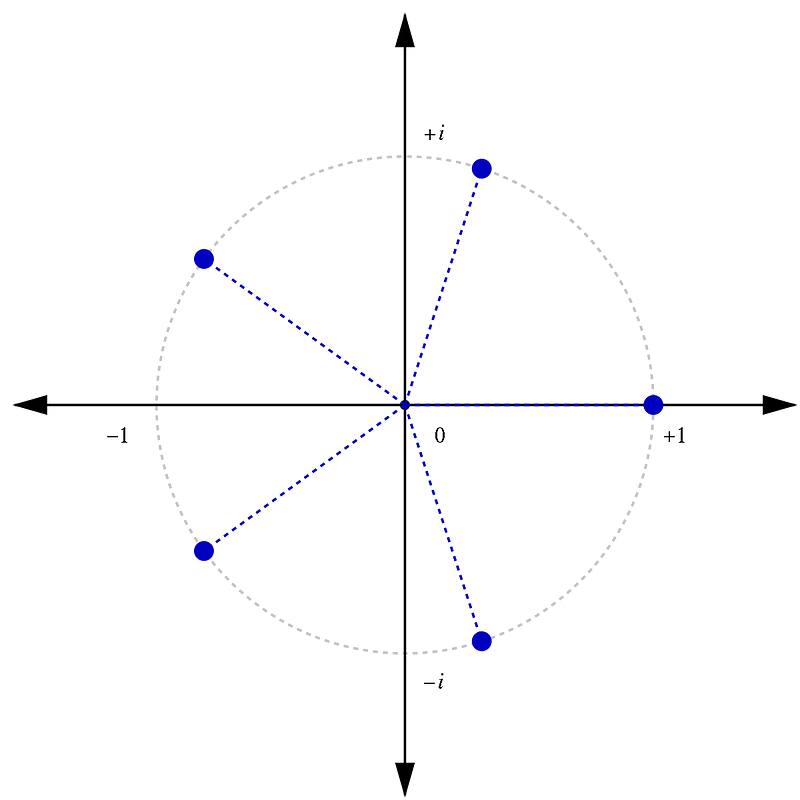
The n roots of unity also form an abelian group under multiplication and exhibit numerous fascinating properties, but that is a topic for another time.
This exploration already reveals that by extending the real numbers into another dimension, many previously hidden mysteries come to light, marking just the beginning of our journey toward enlightenment.
Philosophically speaking, it appears that the imaginary dimension is essential for comprehending various real concepts, such as extracting roots or multiplying by -1.
It seems we were in the dark, struggling to understand concepts in a lower dimension, only perceiving shadows of the actual phenomena. However, this additional dimension illuminates our path, enabling us to grasp these concepts more clearly.
Section 2.4: Contour Integration
This is where the excitement truly begins.
When integrating real functions, we do so over intervals (which may be infinite) of the real line. Given the endpoints, we have limited options regarding the interval, aside from the direction of integration.
In contrast, complex integrals offer a different experience. With two endpoints in the complex plane (which may coincide), we have an infinite array of possible curves (or collections of certain connected curves known as contours) to integrate over, as the domain is two-dimensional.
While this may seem overwhelming and challenging to visualize, it’s not as daunting as it sounds. In fact, for holomorphic functions, an incredible property holds true.
Section 2.5: Cauchy’s Integral Theorem
When two contours (consider them as curves in the complex plane) are selected between the same two endpoints, if we can continuously deform one contour into the other (i.e., they are homotopic), then the integrals along both contours are identical.
This intuitive notion implies that if there are no holes within the domain between the contours, the choice of contour is inconsequential.
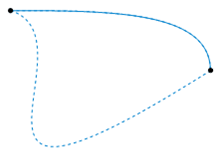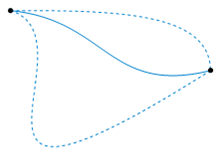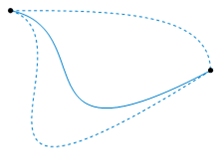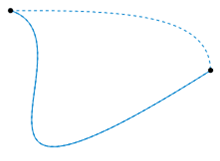
This discovery has intriguing implications rooted in pure topology. For instance, if the endpoints of a contour coincide (resulting in a closed contour), and if the area enclosed by the contour is contractible (homotopic to a single point), then the integral over that contour equals zero. This principle is known as Cauchy’s Theorem, named after Augustin-Louis Cauchy.
Thus, if the function is holomorphic within that domain, the integral evaluates to zero.
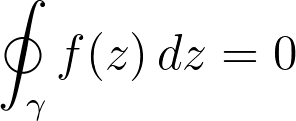
Section 2.6: Meromorphic Functions and the Argument Principle
Recall that holomorphic functions do not possess poles in their domain; they do not exhibit infinite behavior at any points, making them relatively straightforward to work with. However, there are instances where you might want to consider functions that are holomorphic throughout their domain, with the exception of a countable number of points.
These functions are termed meromorphic functions. You can think of them as a generalization of polynomial fractions. The beauty of meromorphic functions lies in their holomorphic properties, even with the presence of poles or singularities. Some of the most significant functions in mathematics, such as the Riemann Zeta Function, the Gamma Function, and 1/z, fall into this category.
Many intriguing questions arise regarding the poles and zeros of these functions, and it turns out that contour integration, combined with the logarithmic derivative, provides a valuable tool for calculating them.
If f is a meromorphic function within and on a closed contour C, and f has no zeros or poles on C, then the following relationship holds:
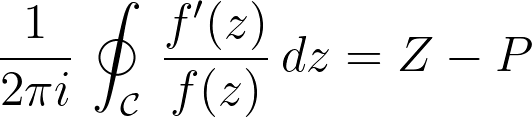
It is fascinating to note that the integral is concerned solely with topology, not geometry! The area and positioning of the curve are irrelevant; what matters is whether it is closed and whether the function possesses poles and zeros within the area inscribed by the contour in the complex plane.
This result connects to a theory known as the calculus of residues, closely related to an extension of Taylor series known as Laurent series, but that is a discussion for another article. You can explore Taylor series here and investigate some intriguing properties of the logarithmic derivative with me here.
Before concluding this section, let’s recap what we’ve learned.
Due to the distinction between geometry and topology in one versus two dimensions, there are stricter restrictions on complex functions than on real functions that need to meet certain limit conditions.
As a result, holomorphic functions exhibit strong properties, rendering them incredibly useful in tackling problems in both complex and real analysis.
Moreover, the field of topology proves beneficial, as complex integrals, known as contour integrals, depend solely on the homotopy equivalence classes of contours, rather than the specific paths themselves.
This understanding paved the way for remarkable discoveries by Augustin-Louis Cauchy and can be employed to calculate the zeros and poles of meromorphic functions, a topic we will explore further.
In the next installment, we will continue to delve into the captivating world of holomorphic and meromorphic functions, as you will discover that they possess properties with implications for quantum physics that remain only partially understood. This exploration involves assigning values to divergent series and extracting profound information from functions, even beyond their defined domains.
Many individuals who encounter mathematics often confuse it with arithmetic, perceiving it as a dry science. In reality, however, it is a discipline that demands a significant degree of imagination.
~ Sofia Kovalevskaya
You will find the next part of this series here.