Chapter 1: A Million-Dollar Challenge in Mathematics

If anyone claims that a career in Mathematics is unprofitable, point them to Grigori Perelman. As of 2019, he stands out as the only individual to have solved a Millennium Prize Problem, achieving fame and a $1,000,000 reward—though he opted to decline the prize.

The problem he tackled, known as the Poincaré Conjecture, relates to the nature of the 3-sphere, which is the hypersphere that encapsulates the unit ball in four-dimensional space.

For those familiar with mathematical jargon: A unit sphere consists of all points at a distance of 1 from a designated central point, typically referred to as the origin (for instance, on a 2D graph, the point (0,0) serves as the origin). A hypersphere, on the other hand, represents points at a constant distance from a given point in an (n-1) dimensional space. In a three-dimensional realm (R³), this would resemble a sphere, or a 2-sphere. A 3-sphere serves as its counterpart in a higher dimension, existing as a hypersphere within the fourth dimension.

Consider a 3-sphere centered at the origin with a radius of 1; it creates a boundary for the unit sphere in this higher dimension. Importantly, if you possess a loop in a Euclidean space that can be continuously tightened to a singular point—imagine reducing a circle's radius until it vanishes—then this loop can be continuously contracted to a point within that space.

In simpler terms, envision a space that resembles ordinary three-dimensional space but is connected, finite, and devoid of edges (a closed 3-manifold). The theorem asserts that if such a space exists, and every loop can be tightened to a point, it is indeed a three-dimensional sphere.

After almost a century of mathematical endeavors, Perelman unveiled his proof between 2002 and 2003. His work built on Richard S. Hamilton's research, which explored the Ricci flow on manifolds to establish certain cases of the Poincaré conjecture. Hamilton's extensive work was unable to conclusively resolve the conjecture. Yet, leveraging this foundational work, Perelman crafted a proof for a broader conjecture known as Thurston’s Geometrization conjecture, thereby completing the Ricci flow program and solving the first Millennium Prize Problem.

On August 22, 2006, the International Congress of Mathematicians honored Perelman with the Fields Medal for his contributions, but similarly to the monetary reward, he declined this honor as well. He humbly remarked that his achievements in proving the conjecture were no more significant than Hamilton's.

The Poincaré Conjecture, along with six other challenging mathematical theories, has been designated as Millennium Prize Problems by the Clay Mathematics Institute (CMI). Each problem is regarded as a crucial question that has remained unresolved over time, with a $1,000,000 reward for the first individual to offer a solution. Nevertheless, as demonstrated, tackling these problems is a formidable challenge. One problem, introduced in 1859 by German mathematician Bernhard Riemann, remains unsolved to this day.

The Riemann Hypothesis, named in honor of Riemann, is widely viewed as the most significant unresolved question in pure mathematics. It holds immense importance in number theory due to its implications regarding the distribution of prime numbers, which are essential in fields ranging from biology to cryptography and quantum mechanics.

To comprehend the Riemann Hypothesis, it’s crucial to grasp a few fundamental concepts: A complex number takes the form a + bi, where i is defined as the square root of -1. In this representation, a is the real part, and bi is the imaginary part. The Riemann zeta function is a function of a complex variable, expressed through the following equation, applicable for any complex number s except 1:

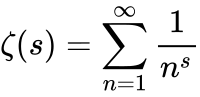
A "zero" of a function refers to an x value such that f(x) = 0. The "trivial zeros" of the Riemann zeta function are all the negative even integers (-2, -4, -6, …), while the "non-trivial zeros" encompass all other s values for which ζ(s) = 0 (i.e., s is not a negative even integer).

Now, here's the statement of the Riemann Hypothesis: The real part of every non-trivial zero of the Riemann zeta function is 1/2. This hypothesis is arguably simpler to grasp than the Poincaré Conjecture and may not initially seem significant. However, it is of great interest to many mathematicians for compelling reasons.

Prime numbers possess a unique property: they cannot be expressed as the product of two smaller integers (e.g., 2, 3, 5, 7, 11, etc.). They are, in a sense, the fundamental building blocks of numbers. Unfortunately, prime numbers do not exhibit a discernible pattern. For example, 3137 is prime, but the next prime number is 3163, followed by a quick succession of other primes (3167 and 3169). Essentially, identifying the next prime requires checking each subsequent number.

However, the Prime Number Theorem (PNT) allows us to estimate the count of prime numbers below a certain limit. This theorem provides estimates but never guarantees certainty. If we assume the Riemann Hypothesis is true, we can combine the PNT with the non-trivial zeros of the Riemann zeta function to refine our error estimates, yielding the best possible bounds for the error term in the PNT. Proving the Riemann Hypothesis could enable the PNT to deliver remarkably accurate estimates, greatly enhancing various branches of mathematics. Numerous significant hypotheses initiate with, "If the Riemann Hypothesis is true, then…," meaning that resolving this problem would validate many subsequent conjectures.

Another intriguing Millennium Problem recently gained attention from the 2017 film "Gifted," which depicted the brother and daughter of a female mathematician dedicated to solving the Navier–Stokes problem. While the movie doesn't delve deeply into the specifics, the problem is nonetheless worthy of exploration.

The Navier-Stokes existence and smoothness problem addresses the mathematical characteristics of solutions to the Navier–Stokes equations, which are foundational to fluid mechanics. Imagine the waves trailing behind a boat on a lake or the turbulent air currents affecting an aircraft in flight. Mathematicians and physicists believe that understanding the solutions to these equations can elucidate and predict both breezy conditions and turbulence.

While the Navier-Stokes existence and smoothness problem encompasses a broad array of questions, the Millennium Problem focuses on one particular assertion: In three spatial dimensions and time, given an initial velocity field, there exists a vector velocity and a scalar pressure field, both of which are smooth and globally defined, that satisfy the Navier–Stokes equations.

To claim success, one must either provide a counter-example or conclusively prove the statement. A resolution to this problem would enhance our understanding of the world, scientifically and in engineering terms. The equations can model weather patterns, ocean currents, water flow in pipes, and airflow around wings, among other applications—ultimately aiding in the design of aircraft and automobiles, studying blood circulation, designing power plants, and analyzing pollution.

There are four additional Millennium Problems, all equally fascinating and difficult to address. However, I prefer to keep my articles concise, so I will reserve discussion of those for another occasion. My personal favorite is the P versus NP Problem, a prominent unsolved question in computer science, which simply asks whether every problem whose solution can be quickly verified can also be solved quickly. While various definitions clarify this statement, it’s a topic for my next article.

For now, if you're intrigued by any of the Millennium Problems or wish to attempt solving one, you can find them listed on the Clay Mathematics Institute website. If you're interested in a more detailed examination of any specific problem, feel free to comment, and let me know which one piques your curiosity!