Successive Differentiation — A Practical Example

Consider the function:

y = f(x) = 5x²

Our goal is to differentiate this function successively as many times as possible. We can apply the power rule, which I have previously discussed in this series.

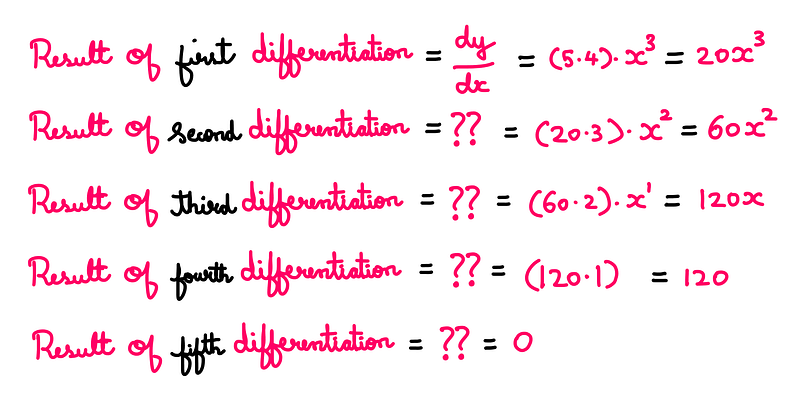
As illustrated, we successfully differentiated the function five times before reaching zero. The outcome of zero indicates that the constant (120) remains unchanged with respect to ‘x’.

In this process, I simply differentiated the results obtained from the original function. This defines successive differentiation—quite straightforward, wouldn’t you agree? However, the next aspect is a bit more intricate.

If you’ve been paying attention, you may have noticed that I used ‘dy/dx’ for the first derivative but simply wrote “??” for the subsequent derivatives. How do we represent these operations, and what do they signify?

Notations for Successive Differentiation

Let’s examine the second derivative, where we differentiate the first derivative (dy/dx) with respect to ‘x’. This can be expressed as follows:

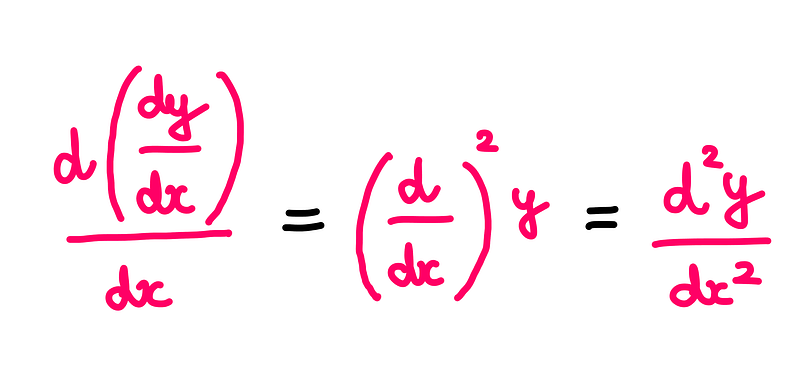
It’s essential to understand that the ‘2’ in this notation is not an exponent but serves as a notation for the order of the derivative.

Gottfried Wilhelm Leibniz, a pioneer in calculus, cleverly manipulated these symbols to function as operators. The ‘d²’ in the numerator does not conform to conventional mathematical definitions, as ‘d’ is neither a variable nor a constant; it functions as an operator.

Historically, mathematicians denoted the denominator as (dx)², but nowadays, ‘dx²’ has become the standard. If we apply this logic to our earlier example, we will derive the following results:

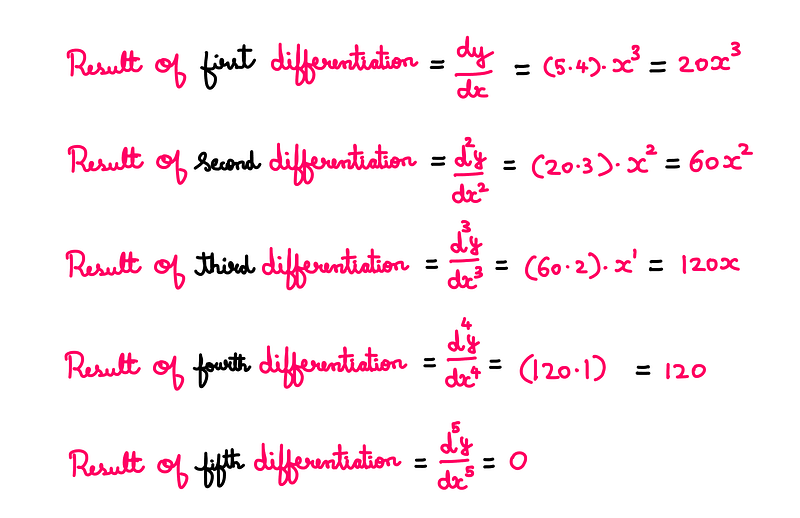
In general terms, the nth derivative of a function ‘y’ with respect to ‘x’ can be represented as:

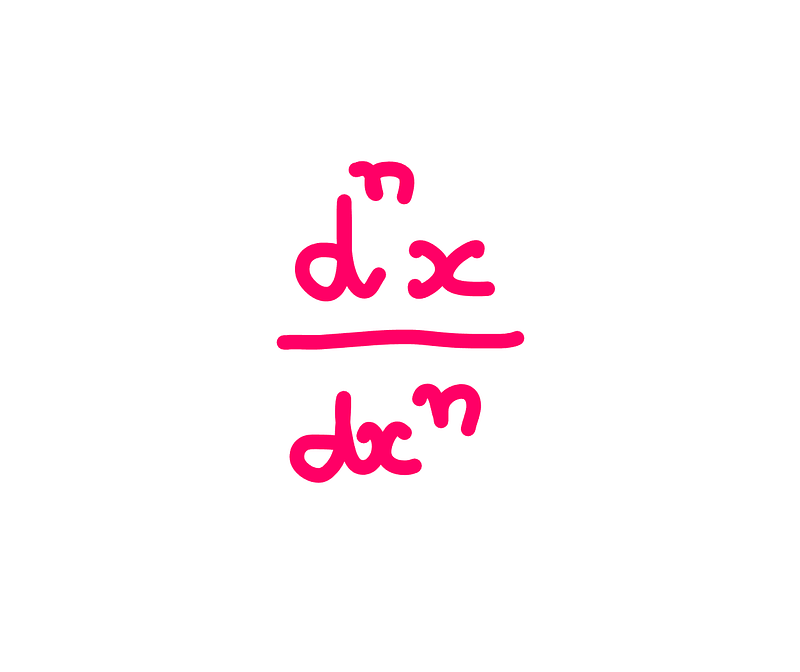
Though practical, writing out all these symbols can be cumbersome. Consequently, mathematicians have developed alternative notation systems for successive differentiation.

Alternative Notations

For the same function, y = f(x), we can also use the following notation for successive differentiation (where f’(x) is pronounced as “f-prime of x”):

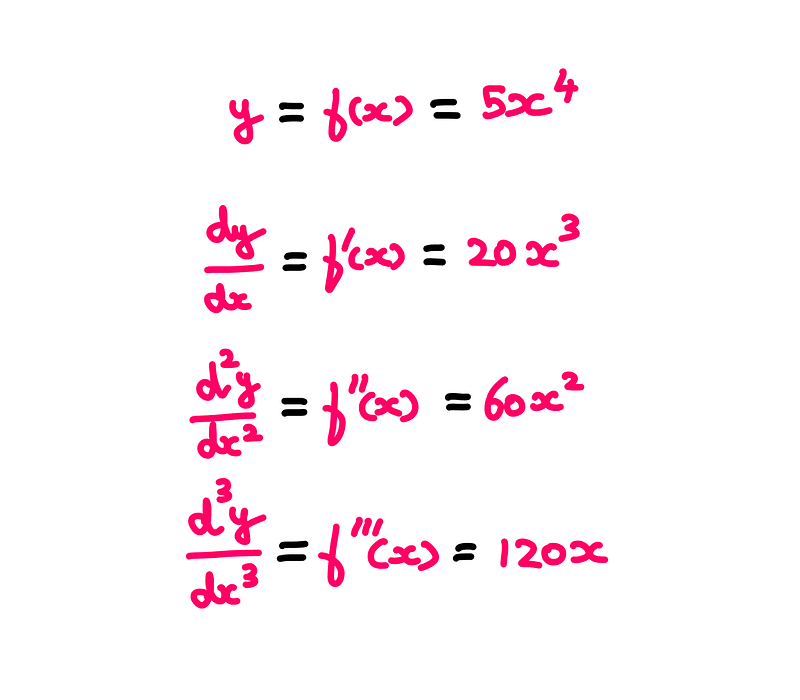
Additionally, in physics, different notations are often used when differentiating variables with respect to time:

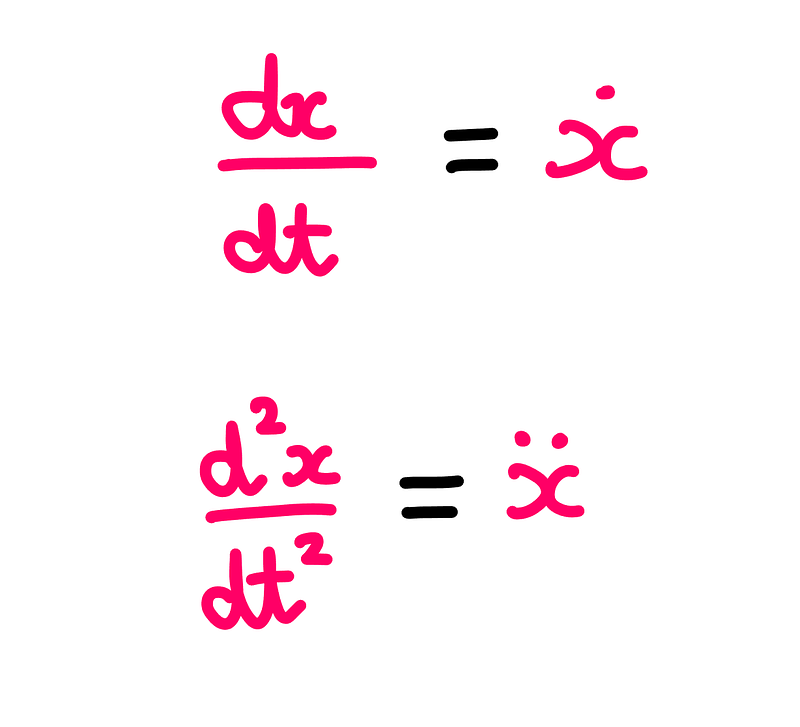
Now that we’ve discussed notation, let’s explore the applications of successive differentiation.

Applications of Successive Differentiation

The primary purpose of successive differentiation is to compute higher-order derivatives. While dy/dx denotes the derivative of ‘y’ with respect to ‘x’, d²y/dx² indicates the second derivative, d³y/dx³ represents the third derivative, and this pattern continues.

If ‘x’ signifies the position of an object as a function of time ‘t’, then dx/dt (the first derivative) illustrates the object's speed over time. Similarly, d²x/dt² indicates the rate at which speed changes over time, known as acceleration. d³x/dt³ represents the change in acceleration, commonly referred to as jerk. Yes, that term is indeed legitimate!

If we continue this process, we encounter terms like snap, crackle, and pop. However, in most scientific contexts, extremely high-order derivatives are rarely necessary. Perhaps this simplicity is a reflection of nature's underlying principles.

On the other hand, the realm of finance, a construct of human invention, often demands higher-order derivatives. When people refer to “astronomical” figures, they might not realize that financial numbers can be even more staggering!

Final Thoughts

By now, it should be clear that the mathematics behind successive differentiation is not overly complex. However, many individuals tend to overlook the significance of the notation and the reasoning behind it.

I hope this discussion has clarified the notations used in successive differentiation and provided insight into its applications. We are currently focused on establishing a solid foundation in calculus, and upcoming essays will delve into increasingly complex concepts. Stay tuned for more enlightening calculus content!

The first video titled "Successive Differentiation" provides an insightful overview of the principles and techniques involved in this mathematical concept.

The second video titled "Formula for the nth Derivative of f(x) = 1/x" elaborates on the formulas used to compute higher-order derivatives, enhancing your understanding of this crucial calculus topic.