Chapter 1: Square Numbers and Their Roots

In our educational journey, we often learn about square numbers such as 1 (=1²), 4 (=2²), 9 (=3²), 16 (=4²), and 25 (=5²). But what occurs when we delve into the square roots of numbers that lie in between these squares? For instance, what are the square roots of 2, 7, and 15? The results are approximately 1.41421356237…, 2.64575131106…, and 3.87298334621…, respectively. The ellipsis at the end is crucial, indicating that these values are non-terminating.

Here’s a more detailed look at the square root of 2: 1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605714701095599716059702745345968620147285174186408891986095523292304843087143214508397626036279952514079896872533965463318088296406206152583523950547457502877599617298355752203375318570113543746034084988471603868999706990048150305440277903164542478230684929369186215805784631115966687130130156185689872372352885092648612494977154218334204285686060146824720771435854874155657069677653720226485447015858801620758474922657226002085584466521458398893944370926591800311388246468157082630100594858704003186480342194897278…

A quick search online reveals that enthusiasts have computed the square root of 2 to millions of decimal places. These numbers are not only non-terminating but also lack any repeating sequence. For comparison, consider the number 1.3434343434… which has a repeating pattern and can be expressed as the fraction 133/99.

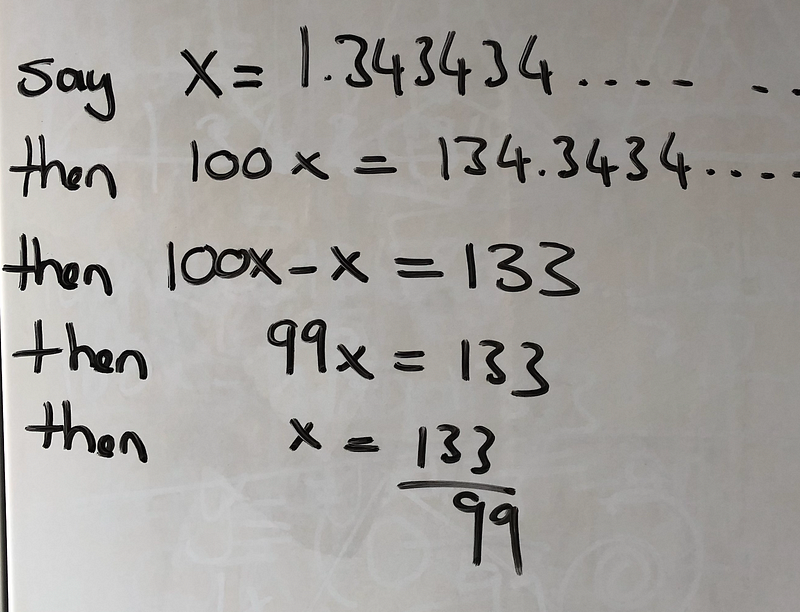
It turns out that the square roots of 2, 7, and 15, as highlighted earlier, are irrational numbers. In mathematics, an irrational number cannot be represented as a fraction p/q where both p and q are integers. Conversely, the fraction 133/99 represents a rational number. Likewise, Pi is also classified as an irrational number.

Furthermore, we can assert that the square root of any non-square number will invariably be irrational. Consider a rational number like 10.44, which equals 1044/100. Squaring it yields precisely 108.9936, which is very close to 109 but not identical! The square root of 109 (not a perfect square) will contain an infinite number of digits after the decimal with no recurring sequence.

If you experiment with squaring decimal numbers on a calculator, you will notice that the result never returns a whole number. So how can we rationalize this phenomenon? Let’s formally present and substantiate the claims made earlier.

Claim: The square root of a positive integer n is rational if and only if n is a square number (i.e., n = m² for some integer m).

Proof: The ‘if’ part is straightforward, but the ‘only if’ part requires more explanation. Assume that the square root of n is rational. This allows us to express it as follows:

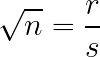
Here, r and s are integers, consistent with our definition of rational numbers. Squaring both sides gives us:

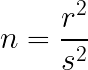
The Fundamental Theorem of Arithmetic, which we will not prove here, states that every number can be expressed as a product of prime numbers, e.g., 10=2*5, 945=3*3*3*5*7. Note that prime factors may repeat, as seen with the number 3 in the latter example.

In our equation for n, we can denote r and s as:

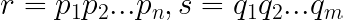
We can then reframe our equation for n as:

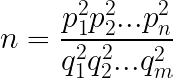
This can be simplified to:

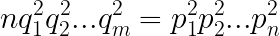
According to the Fundamental Theorem of Arithmetic, the prime factorization of a number is unique. For instance, 10=2*5 cannot be equivalent to the product of any other primes. Similarly, 945=3*3*3*5*7 is not representable as the product of different primes.

Considering both sides of the equation above, we can conclude that n is the product of squared primes. Thus, by taking square roots, we deduce that n is indeed a square number.

In conclusion, square numbers are frequently referred to as perfect squares in mathematics.

Chapter 2: Exploring Square Roots of Non-Square Numbers

The first video, titled "How to Simplify the Square Root of a Non Square Number," provides a detailed explanation on this topic.

The second video, also titled "How to Simplify the Square Root of a Non Square Number," further illustrates these concepts with practical examples.