Understanding Entropy: Measuring Uncertainty in Information
Written on
Chapter 1: Introduction to Entropy
Entropy is a crucial concept in information theory, representing a measure of uncertainty. It underlies essential computer science principles, including the unit of information (bit) and practical applications like data compression and password security. Given that the idea of information transcends computing, I've found numerous real-world applications for entropy, making it a compelling subject to explore in detail.
In this article, we will start by grasping the concept of entropy through straightforward examples. A basic understanding of probability theory will be beneficial as we delve in.
Flipping Coins: A Simple Example
Imagine flipping a fair coin and asking you to predict the outcome. While the result is uncertain, we can be certain that there are two possible outcomes: Heads (H) or Tails (T). In computer terms, each outcome can be represented by a single binary digit (bit), indicating that one bit encapsulates the uncertainty of a single coin flip.
But let's expand this scenario. If I flip two fair coins at once and ask for your guess, we now have four possible outcomes: HH, HT, TH, and TT. Consequently, your chance of guessing correctly is one in four. This introduces us to the realm of probability theory.
Section 1.1: Measuring Information
To quantify the uncertainty in your knowledge while playing this game, we can apply a mathematical framework. When I flipped one coin, you had a 50% chance of guessing right. With two coins, your probability drops to 25%. We can express the uncertainty in your knowledge using the following mathematical representation:

Knowing that P(E) = 0.5 (50%) for the first flip and P(E) = 0.25 (25%) for the second, we can calculate the uncertainty associated with each scenario:
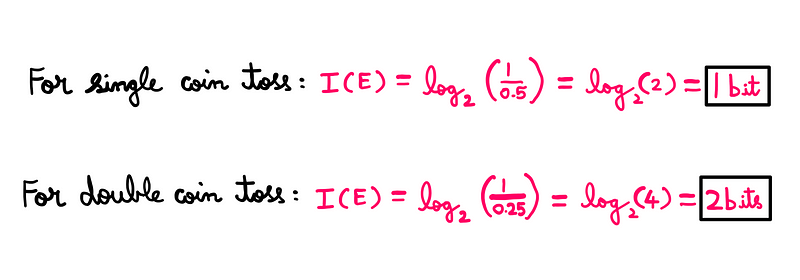
Understanding the Mathematical Framework
The formula we use involves dividing 1 by P(E), which illustrates that a higher probability of a correct outcome correlates with lower uncertainty. For instance, if I were to flip 20 coins, you would recognize that there are 2²⁰ possible outcomes, making your chances of guessing one specific combination exceedingly low.
Additionally, we employ logarithms for two primary reasons:
- They account for the diminishing returns of knowledge: the more we know, the less additional value we derive from that knowledge.
- They provide an intuitive way to measure vast quantities of information, allowing us to compare scales easily.
Using base 2 logarithms aligns perfectly with the binary nature of computers, enabling us to express measures in bits effectively.
Chapter 2: The Concept of Information Content
The term I(E) reflects the level of surprise one might experience when a particular event occurs, often termed Information-content. Essentially, information that does not elicit surprise can be considered "known information," whereas this quantity captures information of genuine significance.
A Slot Machine: Exploring Low Odds
Thus far, we've examined the uncertainty surrounding the event of winning. Conversely, if we analyze the scenario of losing, the calculations yield similar probabilities. However, if we introduce a slot machine with a 1 in 1024 chance of winning, we can evaluate the uncertainty surrounding both outcomes:
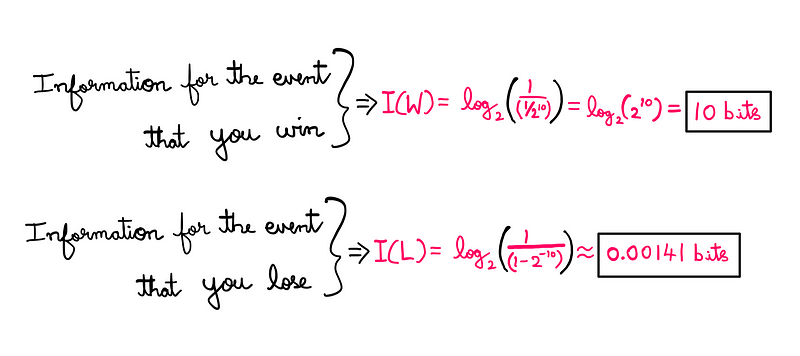
These results affirm that greater uncertainty corresponds to a less likely occurrence. Knowing that losing is the most probable outcome implies minimal uncertainty about that event.
Entropy: Measuring Uncertainty
Entropy can be understood as the average uncertainty in knowledge concerning all potential outcomes of a random event. For the slot machine, we compute entropy as the product of the probability of winning and the associated uncertainty, added to the equivalent for losing:
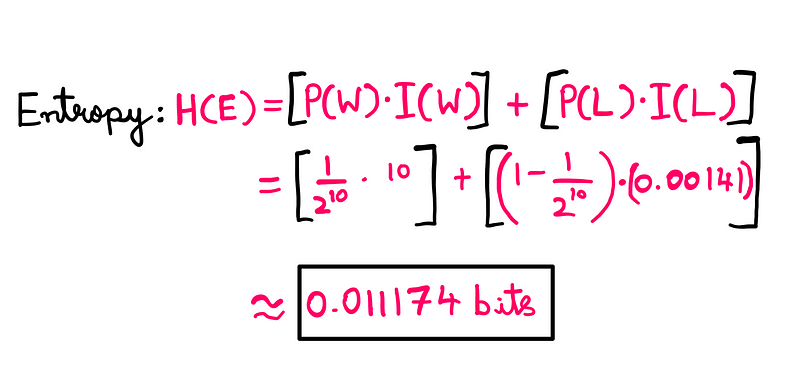
When discussing expected values, it’s crucial to approach the topic with caution. The entropy in the slot machine scenario yields a fractional bit, indicating that while the event's outcome may often require ten bits to convey, there’s a high likelihood that less than one bit suffices.
Applications of Entropy
The insights presented in this essay are rooted in the pioneering work of Claude Shannon, whose contributions laid the groundwork for information theory. To optimize the information conveyed by a slot machine, Shannon proposed that it should only communicate outcomes when a win occurs. This revolutionary idea minimizes resource usage while maximizing the information channel.
This concept has had far-reaching implications, influencing compression algorithms, encryption methods, error-correcting codes, and more. I look forward to discussing these fascinating topics in future writings. For now, I hope this exploration of entropy's fundamentals has been enlightening!
If you appreciate this content, consider supporting my work on Patreon.
References and credit: Claude Shannon and Tim Muller.
You can read the original essay here.