Understanding the Surface Area Formula for Rotational Solids
Written on
Chapter 1: The Rotational Surface Area Formula
The rotational surface area formula, often overlooked in modern education, offers a means to calculate the area of shapes generated by revolving curves around the x-axis. Traditionally a staple in high school math, its presence in curricula seems to be diminishing. This article aims to highlight some intriguing and practical uses of this formula.
Section 1.1: Surface Area of a Sphere Segment
A sphere can be visualized as the result of rotating a circle defined by the equation x² + y² = r² around the x-axis. To find the surface area of a segment of this sphere, sliced between two parallel planes, we can apply our surface area formula.
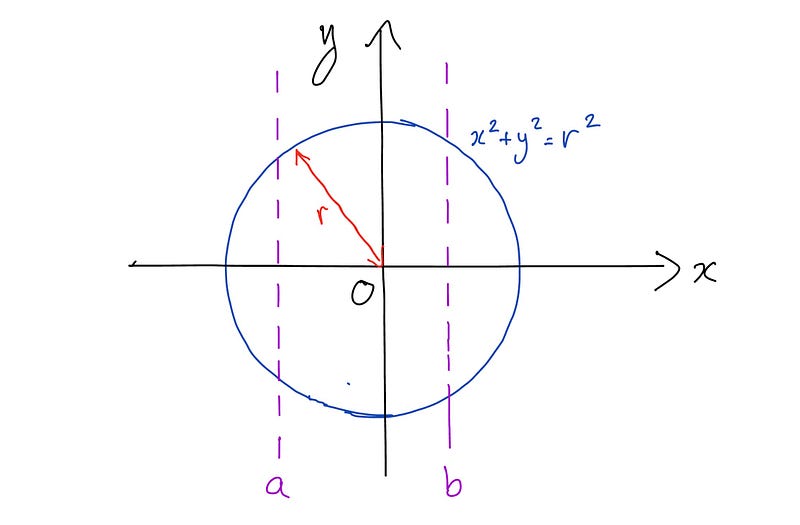
This approach involves integrating the surface area formula between two arbitrary values, a and b, as illustrated in the diagram above. By differentiating the equation of the circle with respect to x, we derive:
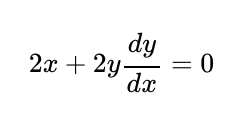
This leads us to:
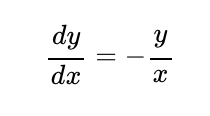
Inserting this into our original formula gives us:
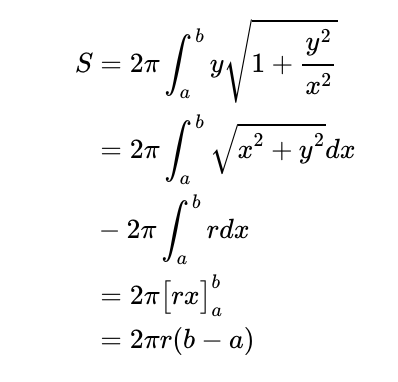
Thus, the surface area of this segment equals 2πr times the perpendicular distance between the two slicing planes. Notably, if we consider the distance to be the diameter of the sphere, we derive the classic surface area formula for a sphere: 4πr².
This video titled "Surface Area of Solid of Revolution (about x-axis, formula explained)" provides a detailed exploration of the formula and its application.
Section 1.2: The Surface Area of an Ice-Cream Cone
An ice-cream cone shape can be created by rotating a circle with a specific radius around the x-axis. To visualize this, we draw a tangent from the origin to a point P on the circle and rotate both the line and the curve segment around the x-axis.
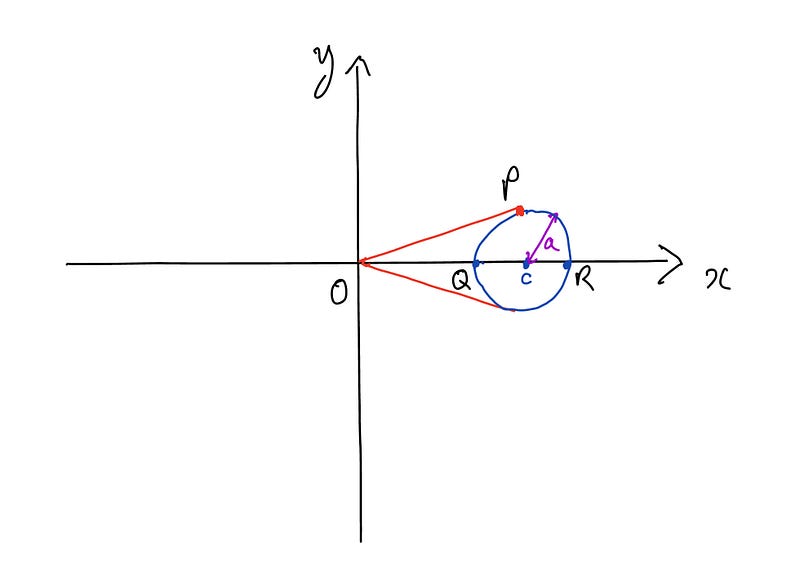
In this case, we consider a circle of radius a centered at (c, 0), with c greater than a. The line segment OP represents the tangent, and the surface area of the cone can be determined by applying our surface area formula to these segments.
Using Pythagorean Theorem, we find that the length of OP is √(c² - a²). This enables us to find the slope and formulate the equation for line OP:
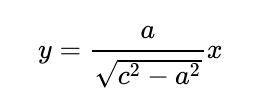
The intersection point P of OP with the circle can be determined using its equation:
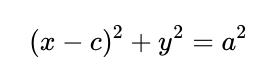
Solving the simultaneous equations yields the x-coordinate of P as (c² - a²)/c. Consequently, we can calculate the surface area of the cone part of the ice-cream cone:
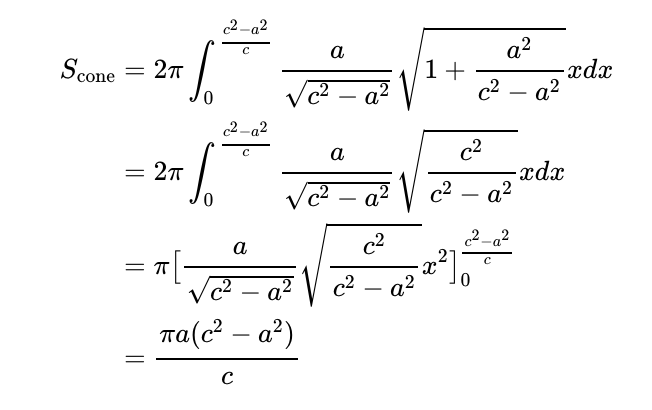
To find the surface area of the "ice cream" portion, which corresponds to the rotation of segment PR, we consider the slice of the sphere between (c² - a²)/c and c + a. This surface area can be calculated as follows:
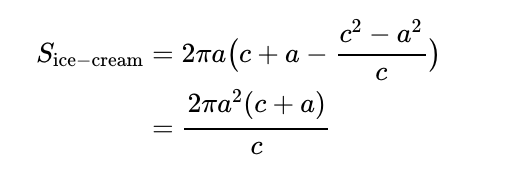
Ultimately, the total surface area of the ice-cream cone becomes:
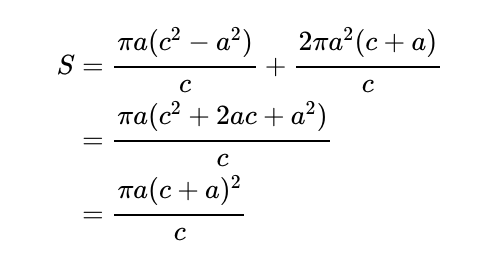
What are your thoughts on this formula? Do you recall learning it during your school years? Are there additional fun applications you can think of?
The second video, "Calculus 2: Area of a Surface of Revolution (Video #9) | Math with Professor V", delves into practical examples and insights related to this formula.