Experience the Thrill of Riding a Rocket Bike!
Written on
Chapter 1: The Rocket Bike Phenomenon
What could be more thrilling than the idea of riding a rocket-powered bicycle? In 2014, François Gissy made this dream a reality. His innovative creation allowed him to reach an astonishing speed of 333 km/hr in just 4.8 seconds—an impressive feat indeed. He even raced against a Ferrari and left it in the dust. Watch the exhilarating moment below:
Tragically, François later lost his life while testing another rocket bike. However, we can pay tribute to his legacy by exploring some fascinating physics concepts based on his remarkable ride.
Section 1.1: The Acceleration Experience
Imagine being on a rocket bike as it accelerates rapidly. While acquiring position-time data through video analysis can be challenging, we can rely on the numbers shared in the footage. Here are the key statistics: an acceleration from 0 to 333 km/hr (92.5 m/s) over 4.8 seconds, producing a thrust of 4.51 kN, a peak acceleration of 3.05 g (29.89 m/s²), and an average acceleration of 1.96 g (19.2 m/s²). Note that the term “deceleration” is not one I prefer to use.
These values were likely gathered using onboard sensors, so we can trust them. Let's quickly verify the average acceleration based on the formula for one-dimensional acceleration.
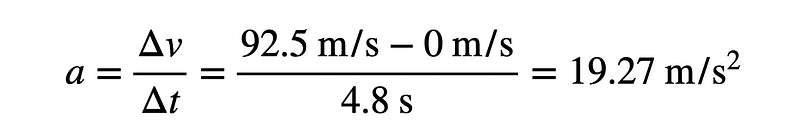
Section 1.2: Understanding the Forces
Now, let’s delve into the forces at play. Here’s a diagram illustrating the interactions experienced during the ride.
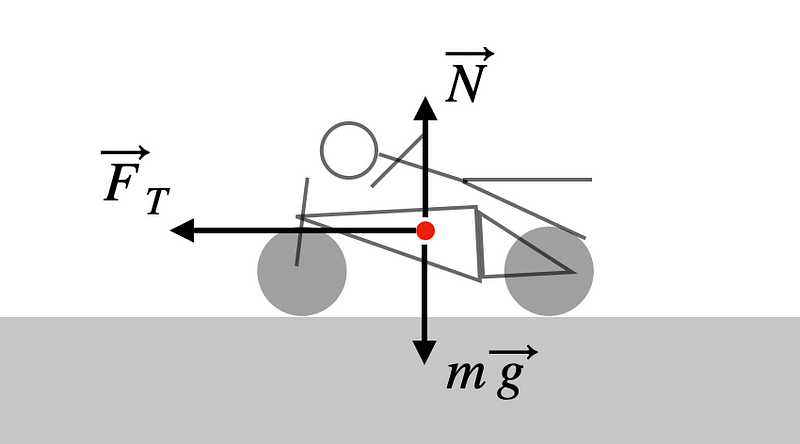
This force diagram represents the bike-rider system as a single unit. The rocket exerts a force on the bike, propelling it forward. However, the bike's acceleration is what propels the rider. If we assume the rider weighs 75 kg, we can calculate the bike's force using the maximum acceleration of 29.89 m/s².
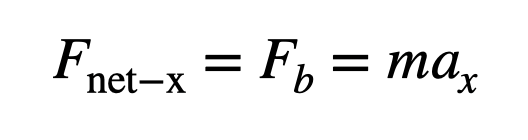
Plugging in the weight and acceleration, we find that the bike generates a force of 2242 Newtons (equivalent to 504 pounds). If you were merely gripping the handlebars, it would feel as if you were suspended with extra weight on your back. Thankfully, the rider benefits from additional support—he's not just holding onto the handlebars, as the back seat also aids in keeping him secure.
Chapter 2: Comparing Speeds with Cars
Now, why does this rocket bike outpace a Ferrari, a car known for its remarkable speed due to a powerful 600-horsepower engine? The answer lies in the forces propelling each vehicle. The rocket bike benefits from rocket thrust, while the car relies on friction between its tires and the road.
To model the frictional force between two surfaces, we can use the following formula (applicable for static friction when both surfaces are stationary).
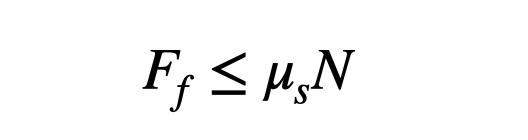
The maximum frictional force (according to this model) is derived from multiplying the coefficient of friction (µ) by the normal force (N). Assuming the bike is on a level surface, the normal force equals its weight. Thus, the maximum acceleration would be:
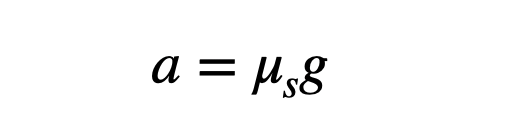
Even with a coefficient of 1, the maximum acceleration would be limited to 9.8 m/s²—far lower than what the rocket bike achieves.
Section 2.1: The Impact of Air Resistance
One intriguing aspect is air drag. When the rocket's thrust was deactivated, the bike experienced an acceleration of -13.72 m/s² opposite to its motion, indicating the effect of air resistance.
The force of air resistance can be complex, but we can employ a model that generally fits.
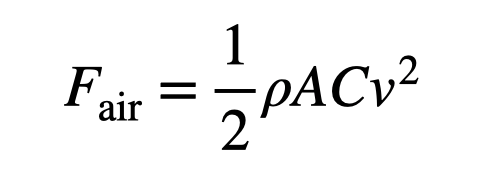
In this equation, ρ represents air density, A is the cross-sectional area, C is the drag coefficient, and v is the velocity. For the rocket bike, most variables remain constant except for the velocity. We can express the air force as:
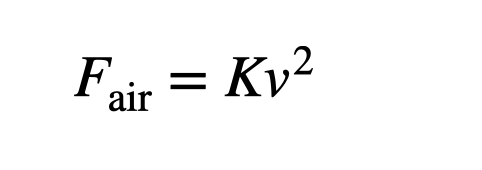
At maximum speed (9.5 m/s), air resistance becomes the only force acting on the bike in the x-direction. To find the constant K, we return to the beginning of the run, where the bike was stationary, meaning air drag was negligible, and thrust was the only force at play. Using this data, I estimated the combined mass of the rocket bike and rider to be 150.9 kg, which seems plausible.
Though the mass decreases as fuel is consumed, we can treat it as relatively constant for our calculations. Utilizing the post-thrust acceleration of -13.72 m/s² and a velocity of 92.5 m/s, we derive a K value of 0.242 kg/m.
Now equipped with this knowledge, we can model the entire ride. I’ll assume that the rocket's thrust remains constant at 4.51 kN throughout the 4.8 seconds, while air drag increases with speed. This leads to the formula for the bike's acceleration:
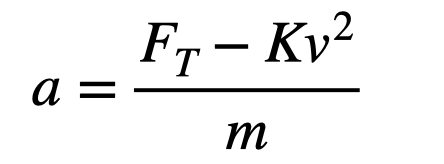
Normal kinematic equations won’t suffice here, as the acceleration isn't constant. Instead, we can break the problem down into tiny time intervals and assume constant acceleration during each interval, implementing a numerical approach.
I'll skip the intricate details (but if you're interested, here is the code). Below is my model depicting the rocket bike's motion, showcasing velocity versus time.
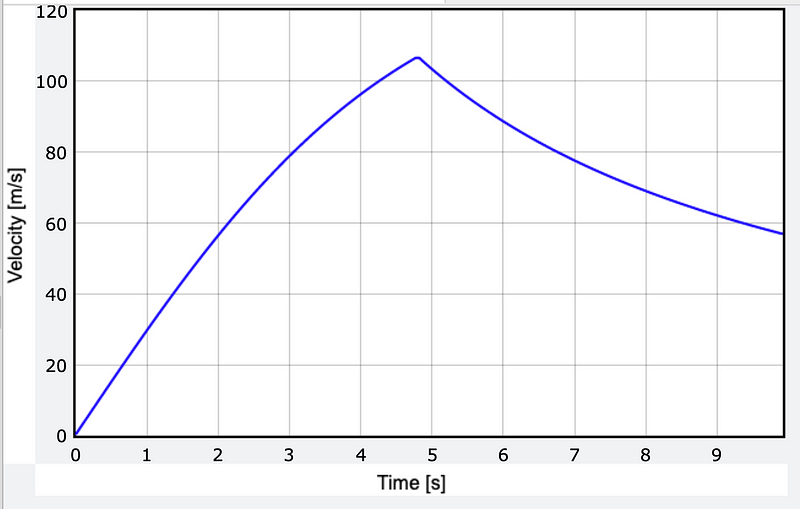
I'm pleased with the results, which indicate a maximum speed slightly exceeding 92.5 m/s. The discrepancy may arise from the assumption that thrust is constant, but overall, the model aligns well with reality.