Chapter 1: An Intriguing Calculus Challenge

I find this problem particularly enjoyable, and I managed to solve it rather quickly. You really only need a grasp of high school calculus along with some algebraic skills!

Here’s a little hint: think about the difference of squares…

I encourage you to pause here, take out a pen and paper, and try to solve it yourself. Once you’re ready, continue reading for the solution!

These engaging puzzles may not be the most complex, but they bring me joy every time I successfully navigate through them.

Let’s begin by integrating the function, which is simply the anti-derivative of x.

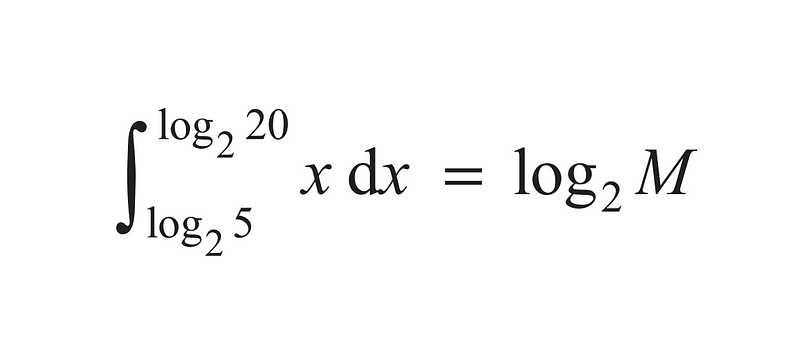
Next, we will substitute the limits into the equation.

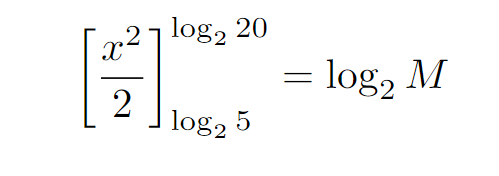
Do you recall the difference of squares formula from your school days?

Here it is:

a² - b² = (a + b)(a - b)

Now, let’s apply this to our equation.

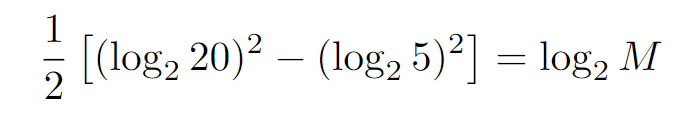
When logarithms share the same base, addition converts to multiplication, and subtraction also converts to multiplication.

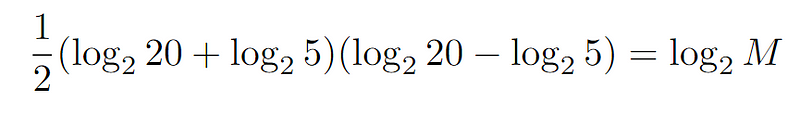
For instance, 20 multiplied by 5 equals 100, and 20 divided by 5 results in 4.

This leads us to conclude that 2 raised to the power of 2 gives us 4, hence log2(4) equals 2.

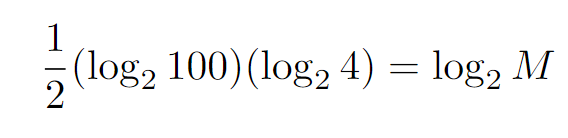
In the end, we can simplify by eliminating the 2 and 1/2.

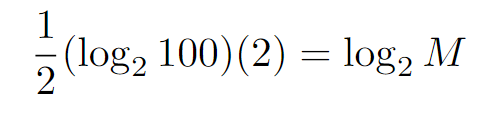
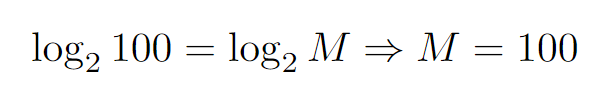
How fascinating was that?

What was your thought process while solving it? Please share your insights in the comments; I’m eager to hear from you!

Math Puzzles to Explore

Discover a collection of the finest math puzzles available on Medium, covering topics from Algebra and Geometry to Calculus and Number Theory. Don’t hesitate to share this with your friends!

The first video, How to Determine What M and B Are in y = mx + b, provides a clear explanation of finding the slope and y-intercept in linear equations.

The second video, Finding the Equation of a Line from a Graph (y = mx+b), demonstrates how to derive the equation of a line using graphical methods.

Thank you for taking the time to read this! If you found the information valuable, please show your appreciation by giving this article a clap.

If you enjoy my content and wish to support my work, consider buying me a coffee. Your generosity helps sustain my writing endeavors and academic pursuits.

Happy Solving, Bella