Chapter 1: Understanding Cubic Roots

In this discussion, we delve into a fundamental method of approximating cubic roots through the principles of architectural symmetry and the properties of similar triangles. This technique enhances intuitive grasping of cubic polynomials and, with some adjustments, can be applied to more complex polynomial equations. This article builds upon a previous exploration titled "Cubic Polynomials — Using Similar Triangles to Approximate Roots," which emphasized the utility of similar triangles derived from turning points and inflection points.

The advantages and disadvantages of these methods are challenging to summarize succinctly; however, the latter approach is particularly advantageous. It can be easily formulated and does not require advanced calculus beyond identifying the inflection point (Ip). This method is particularly effective when Ip(x)=B/3A<1, especially with high coefficients for x, resulting in steeper transitions between turning points.

This discussion assumes a foundational understanding of high school-level mathematics.

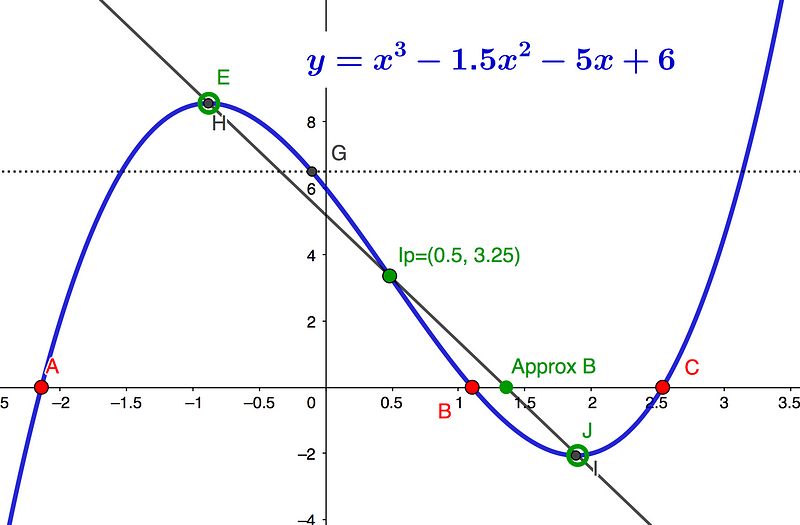
As we explore the simplest cubic root, it is vital to understand the relationship between the shrinking chord and the turning points as it approaches the x-axis, nearing the target root B, as illustrated in Diagram 1 with the function example y=x³-1.5x²-5x+6. The point G is rotationally symmetrical with respect to root B.

Section 1.1: The Mechanics of the Shrinking Chord

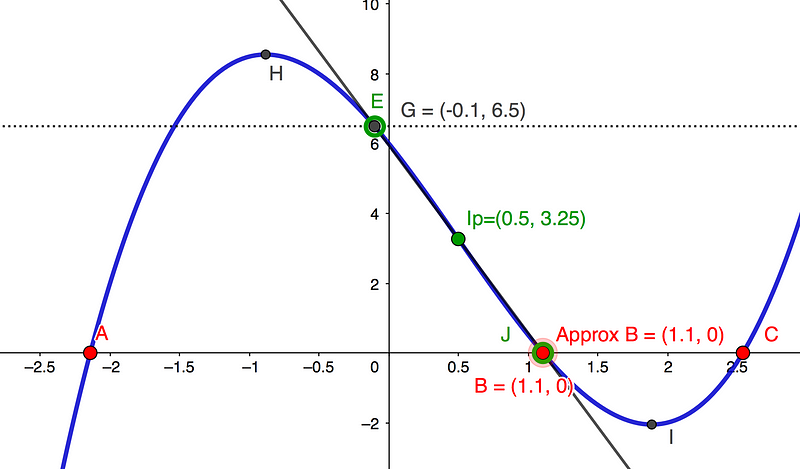
As the chord diminishes, it rotates clockwise around the inflection point (Ip) until intercept E aligns with point G (which is undefined). This relationship is depicted in Diagram 2, where intercept J and the approximate root B converge with root B. Thus, we can conclude:

Approximate Root B equals Root B precisely when E equals G.

Subsection 1.1.1: Formula for Approximate Roots

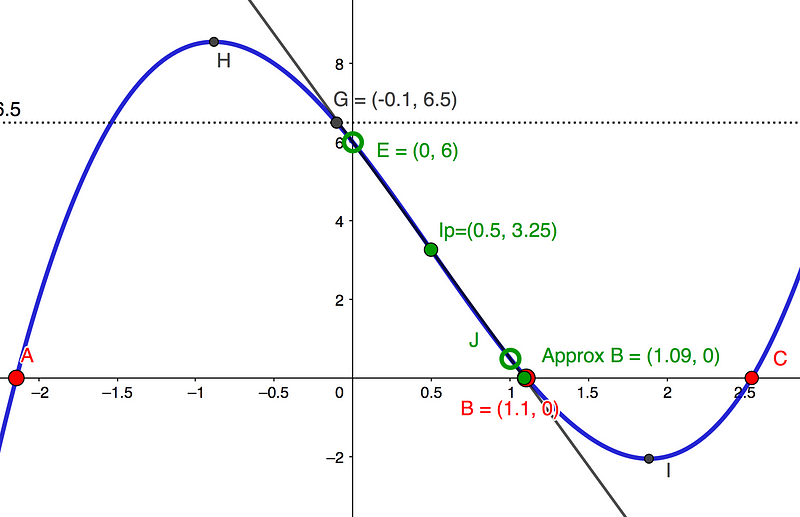
Given that the x-coordinate of point G remains unknown, we can utilize a nearby constant value, D=6, and apply the similar triangles principle to derive Approximate Root B. Referencing Diagram 3, we can express this as follows:

Approximate Root B = Ip(x) * D / (D - Ip(y)), leading to:

Approximate Root B = 0.5 * 6 / (6 – 3.25) = 1.09, which closely matches the actual value of 1.1.

Section 1.2: Finding Remaining Roots

To finalize our work, the second and third roots can be easily derived using the "Extended Quadratic Equation" referenced in my previous article, "Cubic Polynomials—A Simpler Approach."

Chapter 2: Summary of Findings

This video explains how to simplify cube roots, providing a foundational understanding of the topic.

This video addresses the simplification of cube roots, including perfect cubes and more challenging examples.

In summary, this article presents a method utilizing similar triangles within the symmetry of cubic polynomials to discover the "Simplest Root." This approach effectively connects mathematical concepts with graphical interpretations, allowing mathematics to serve your understanding, rather than the other way around!