Chapter 1: Understanding the Probability Challenge

Imagine a scenario where a ball is dropped into a lucky draw machine, as depicted in the image below. Upon hitting a nail, the ball randomly diverts either to the left or to the right.

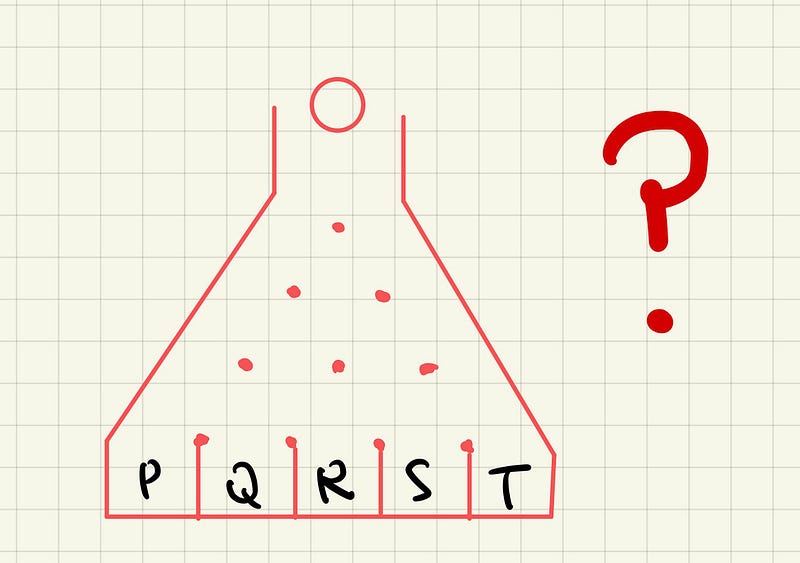
Can you calculate the probability of the ball landing in box Q? Take a moment to pause, grab a pen and paper, and give it a shot. Once you're ready, continue reading for the solution!

Solution Approach

To tackle this problem, we should examine the possible paths the ball may take as it interacts with the nails. We will denote the ball going left as L and right as R.

Through a process of trial and error, we can outline various potential outcomes:

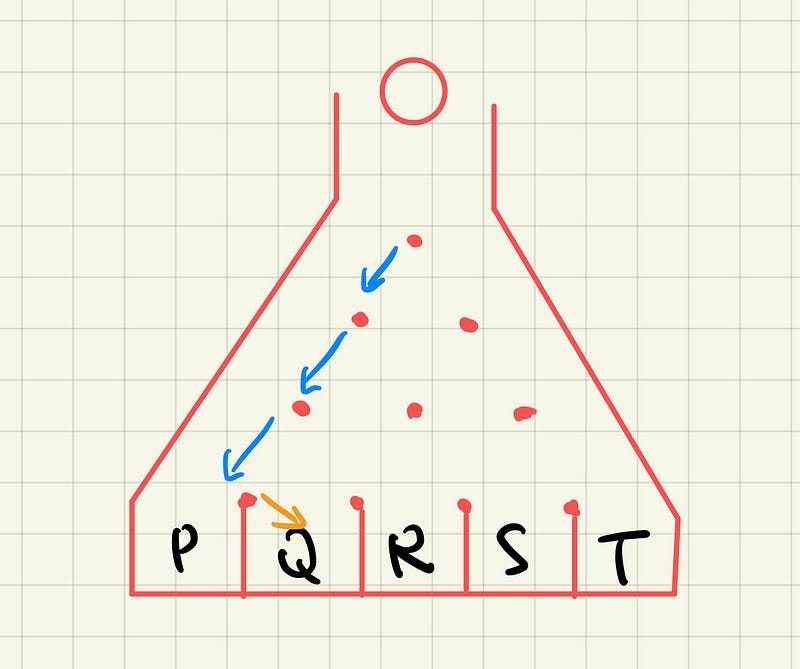
Case 1: LLLR

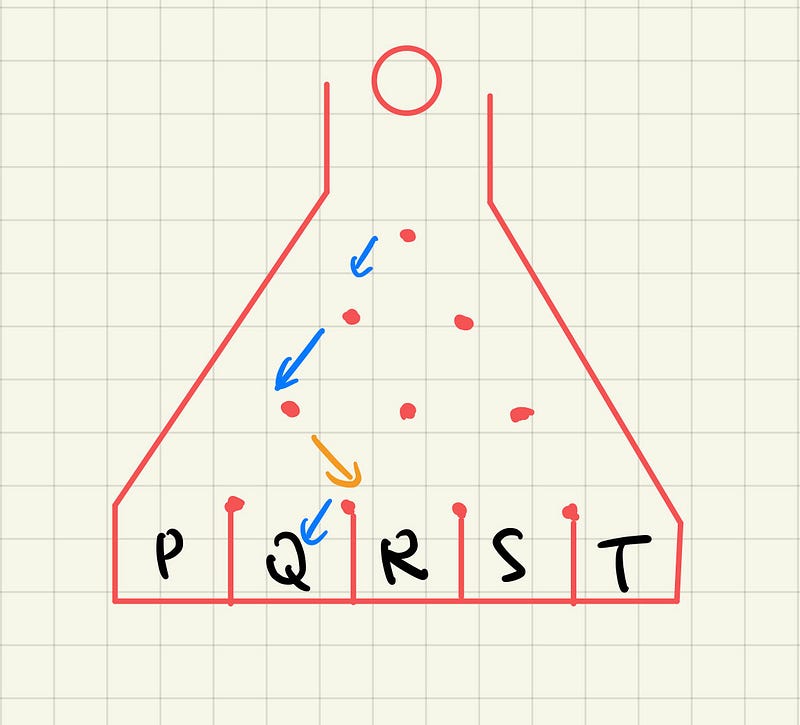
Case 2: LLRL

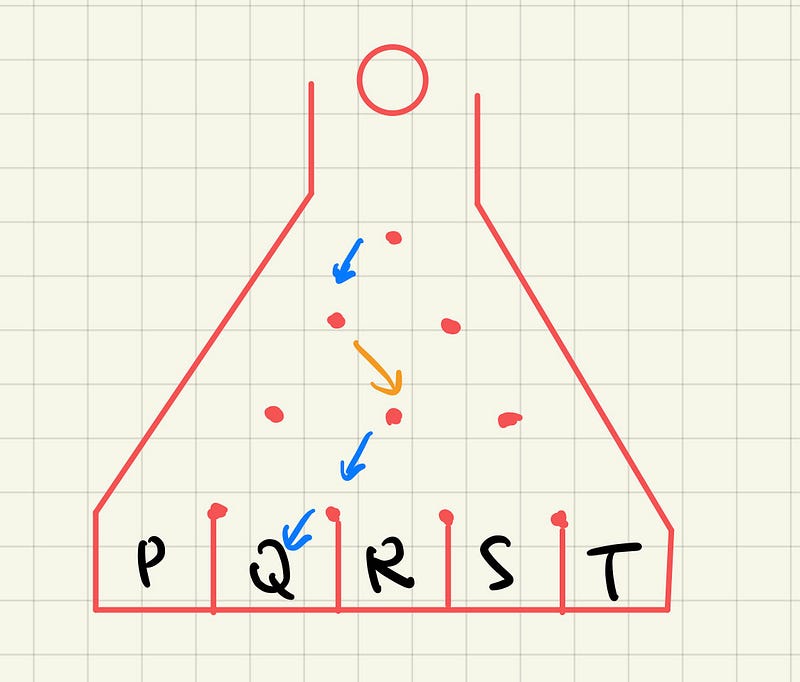
Case 3: LRLL

Case 4: RLLL

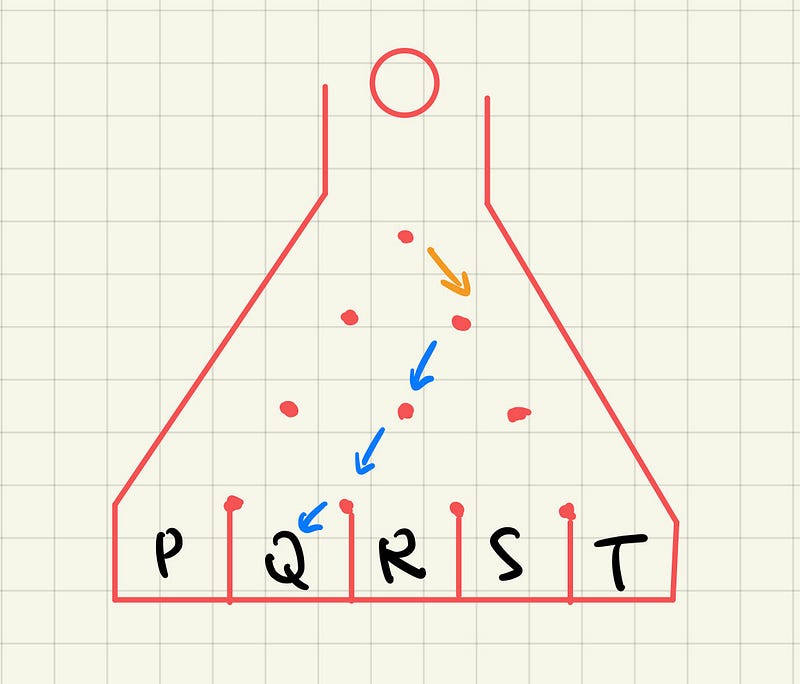
Given that the ball has two options at each of the four stages—either left or right—we can deduce that there are a total of (2^4 = 16) possible outcomes. Among these outcomes, the ball successfully lands in box Q in 4 instances. Thus, the probability can be calculated as ( frac{4}{16} = frac{1}{4} ).

Incredible, isn't it?

What did you think of this exercise? Feel free to share your thoughts in the comments below; I'm eager to hear your insights!

Chapter 2: Enhance Your Math Skills

For those looking to elevate their mathematical prowess, I invite you to explore these resources.

The first video, "HOW TO PLAY 9-BALL - The 'Official Rules' of Pool," provides an engaging overview of the game’s fundamental strategies.

The second video, "FOULS IN POOL ... Everything You Need to Know," covers essential rules and common mistakes that players should avoid.

Don't forget to share this list of exciting math puzzles with your friends and fellow enthusiasts!

Thank you for your time! If you found this article beneficial, please show your appreciation by giving it a clap.