Eliminating Rectangles from a Square Grid: A Mathematical Challenge
Written on
Understanding the Problem
In a captivating challenge from the 2023 China Girls Math Olympiad, we are tasked with determining the minimum number of sticks to remove from the edges of squares on an 8 by 8 chessboard, ensuring no rectangles remain. This problem exemplifies the fascinating nature of chessboard-related mathematical inquiries and presents a delightful puzzle for enthusiasts of all ages.
To tackle this conundrum effectively, it can be helpful to start with smaller configurations.
Starting with Smaller Grids
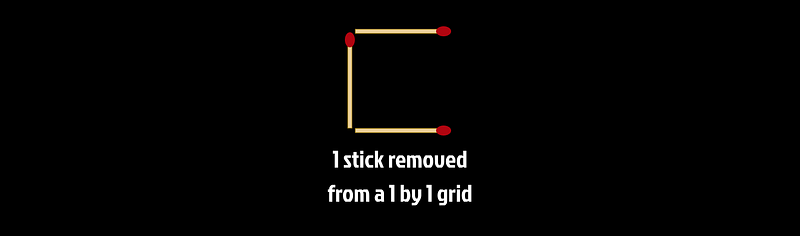
Let’s examine a basic scenario: a 1 by 1 grid. In this case, only one stick needs to be removed to prevent any rectangles from forming.
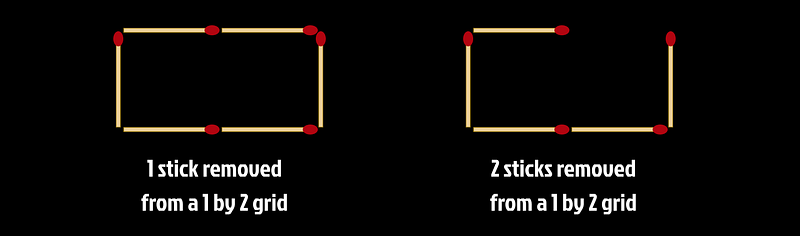
Next, consider a 1 by 2 grid. This layout initially consists of three rectangles: two individual unit squares and the overall 1 by 2 rectangle. Here, removing just one stick won't suffice; you'll need to remove two sticks for complete rectangle elimination.
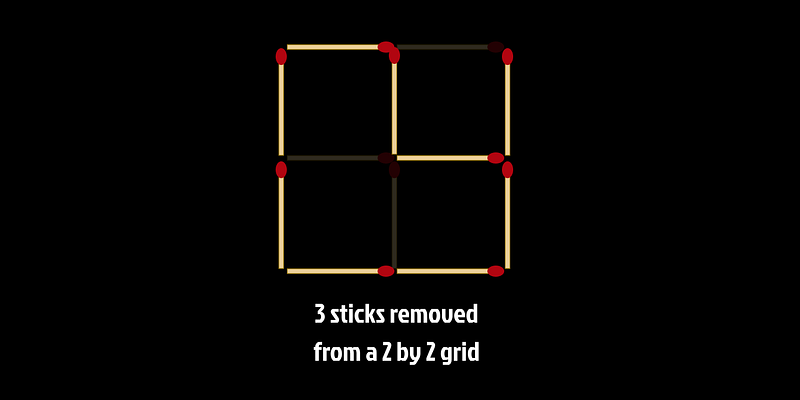
Now, let’s analyze a 2 by 2 grid. This configuration contains four unit squares, four 1 by 2 rectangles, and one encompassing 2 by 2 square. Surprisingly, removing just three sticks is enough to eliminate all nine potential rectangles!
Generalizing to Larger Grids
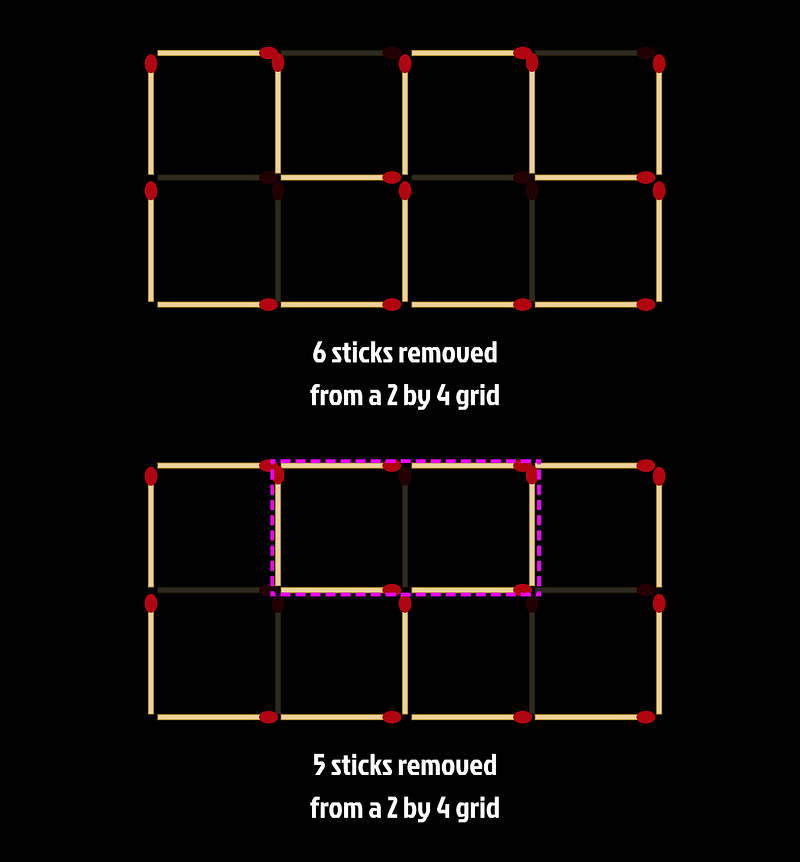
Expanding our perspective, when we place two 2 by 2 grids side by side, we create a 2 by 4 grid without any rectangles, which requires six sticks to be removed. Notably, it is impossible to achieve this with only five removals, as sharing a stick between adjacent grids would inevitably form a 1 by 2 rectangle.
Continuing this approach, arranging four 2 by 2 grids results in a 4 by 4 grid, where only twelve sticks need to be removed to maintain rectangle-free status.
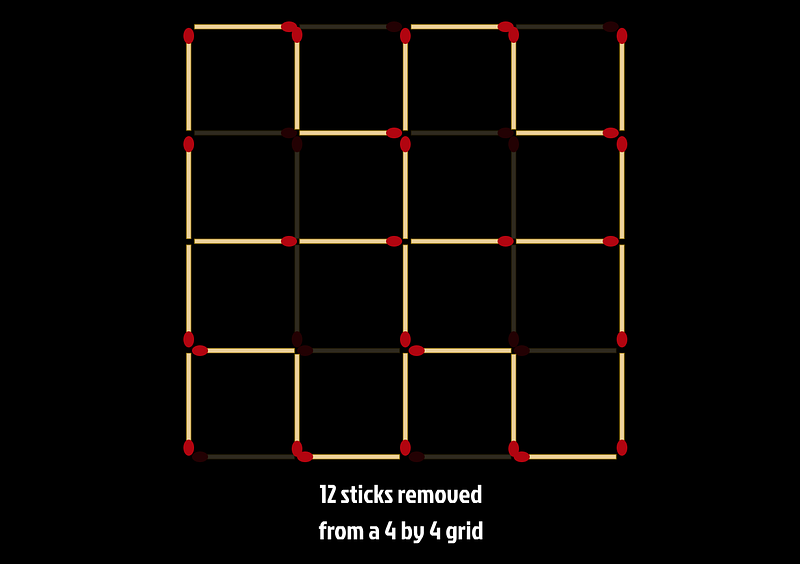
Following this logic, one might believe that arranging four 4 by 4 grids would yield an 8 by 8 grid with no rectangles, needing only 48 sticks to be removed. However, this assumption would lead to an unexpected conclusion.

A surprising revelation is that only 11 sticks are required to ensure a 4 by 4 grid remains rectangle-free. This contradiction arises from the flawed assumption that each 2 by 2 grid must have three sticks removed, which is not universally applicable.
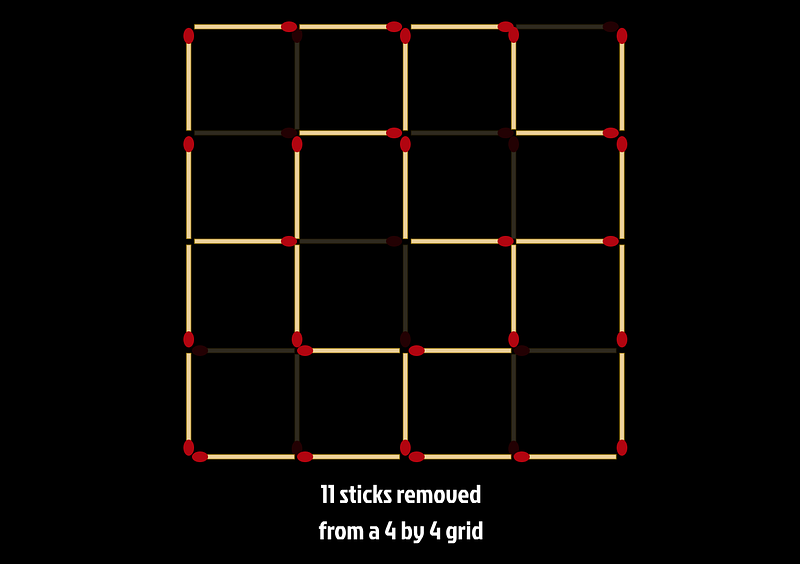
The arrangement of L-shaped blocks of three squares proves to be more efficient than initially thought. Each configuration leverages these blocks, allowing for a unique distribution of stick removals.
Building a Solution for the 8 by 8 Grid
When expanding to the 8 by 8 grid, the top right section contains one single square with a removed stick, while the remainder consists of L-shaped blocks. This arrangement results in a total of 43 sticks being removed.

The arrangement demonstrates that for each block of three squares, at least two sticks must be removed to prevent the formation of any rectangles, solidifying that 43 removals is indeed the optimal solution.

This problem presents an intriguing exploration of mathematical principles and encourages further investigation into similar challenges.